



Next: Cosine Measure
Up: Similarity Measures for Document
Previous: Similarity Measures for Document
Contents
Conversion from a Distance Metric
The Minkowski distances
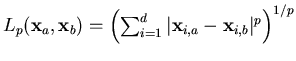 are the standard metrics for geometrical problems. For
are the standard metrics for geometrical problems. For 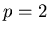 we obtain
the Euclidean distance. There are several possibilities for converting
such a distance metric (in
we obtain
the Euclidean distance. There are several possibilities for converting
such a distance metric (in 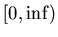 , with 0 closest) into a
similarity measure (in
, with 0 closest) into a
similarity measure (in ![$ [0,1]$](img298.png) , with 1 closest) by a monotonic
decreasing function. For Euclidean space, we chose to relate
distances
, with 1 closest) by a monotonic
decreasing function. For Euclidean space, we chose to relate
distances 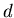 and similarities
and similarities 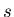 using
using
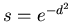 . Consequently,
we define Euclidean [0,1]-normalized similarity as
. Consequently,
we define Euclidean [0,1]-normalized similarity as
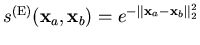 |
(4.1) |
which has important desirable properties (as we will see in the
discussion) that the more commonly adopted
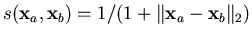 lacks.
Other distance functions can be used as well. The Mahalanobis distance
normalizes the features using the covariance matrix. Due to the
high-dimensional nature of text data, covariance estimation is
inaccurate and often computationally intractable, and normalization is
done if need to be, at the document representation stage itself,
typically by applying TF-IDF.
lacks.
Other distance functions can be used as well. The Mahalanobis distance
normalizes the features using the covariance matrix. Due to the
high-dimensional nature of text data, covariance estimation is
inaccurate and often computationally intractable, and normalization is
done if need to be, at the document representation stage itself,
typically by applying TF-IDF.




Next: Cosine Measure
Up: Similarity Measures for Document
Previous: Similarity Measures for Document
Contents
Alexander Strehl
2002-05-03
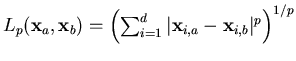 are the standard metrics for geometrical problems. For
are the standard metrics for geometrical problems. For 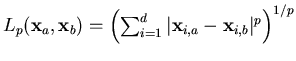 are the standard metrics for geometrical problems. For
are the standard metrics for geometrical problems. For ![]() we obtain
the Euclidean distance. There are several possibilities for converting
such a distance metric (in
we obtain
the Euclidean distance. There are several possibilities for converting
such a distance metric (in ![]() , with 0 closest) into a
similarity measure (in
, with 0 closest) into a
similarity measure (in ![]() , with 1 closest) by a monotonic
decreasing function. For Euclidean space, we chose to relate
distances
, with 1 closest) by a monotonic
decreasing function. For Euclidean space, we chose to relate
distances ![]() and similarities
and similarities ![]() using
using
![]() . Consequently,
we define Euclidean [0,1]-normalized similarity as
. Consequently,
we define Euclidean [0,1]-normalized similarity as