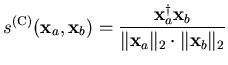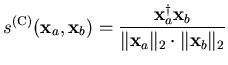Next: Pearson Correlation
Up: Similarity Measures for Document
Previous: Conversion from a Distance
Contents
Cosine Measure
A popular measure of similarity for text (which
normalizes the features by the covariance matrix)
clustering is the
cosine of the angle
between two vectors. The cosine measure is given by
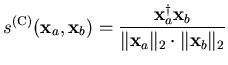 |
(4.2) |
and captures a scale invariant understanding of similarity. An even
stronger property is that the cosine similarity does not depend on the
length:
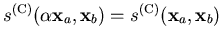 for
for
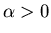 . This allows documents with the same composition, but
different totals to be treated identically which makes this the most
popular measure for text documents. Also, due to this property,
samples can be normalized to the unit sphere for more
efficient processing
[DM01].
. This allows documents with the same composition, but
different totals to be treated identically which makes this the most
popular measure for text documents. Also, due to this property,
samples can be normalized to the unit sphere for more
efficient processing
[DM01].
Alexander Strehl
2002-05-03