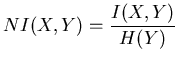Next: Bibliography
Up: Derivations
Previous: Normalized Symmetric Mutual Information
Contents
Normalized Asymmetric Mutual Information
The entropy of either, clustering 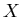 and categorization
and categorization 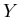 , provides
another tight bound on mutual information
, provides
another tight bound on mutual information 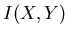 that can be used
for normalization. Since the categorization
that can be used
for normalization. Since the categorization 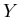 is a stable, user
given distribution, let's consider
is a stable, user
given distribution, let's consider
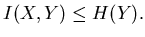 |
(8.10) |
Hence, one can alternatively define [0,1]-normalized asymmetric
mutual information based quality as
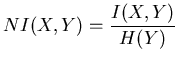 |
(8.11) |
which translates into frequency counts as
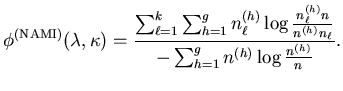 |
(8.12) |
Note that this definition of mutual information is asymmetric and does
not penalize overrefined clusterings
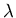 . Also,
. Also,
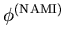 is biased towards high
is biased towards high  .
.
Alexander Strehl
2002-05-03
![]() and categorization
and categorization ![]() , provides
another tight bound on mutual information
, provides
another tight bound on mutual information ![]() that can be used
for normalization. Since the categorization
that can be used
for normalization. Since the categorization ![]() is a stable, user
given distribution, let's consider
is a stable, user
given distribution, let's consider