



Next: Normalized Asymmetric Mutual Information
Up: Derivations
Previous: Derivations
Contents
Normalized Symmetric Mutual Information
Let 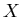 and
and 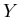 be the random variables described by the cluster
labeling
be the random variables described by the cluster
labeling
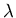 and category labeling
and category labeling
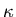 ,
respectively.
Let
,
respectively.
Let 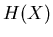 denote the entropy of a random variable
denote the entropy of a random variable 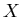 .
Mutual information between two random variables
is defined as
.
Mutual information between two random variables
is defined as
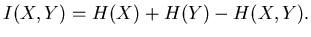 |
(8.1) |
Also,
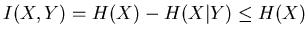 |
(8.2) |
and
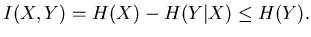 |
(8.3) |
So
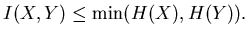 |
(8.4) |
Since
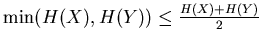 , a tight upper bound
on
, a tight upper bound
on 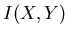 is given by
is given by
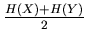 . Thus, a worst case
upper bound for all possible labelings A (with labels from 1 to
. Thus, a worst case
upper bound for all possible labelings A (with labels from 1 to  )
and categorizations (with labels from 1 to
)
and categorizations (with labels from 1 to 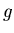 ) is given by
) is given by
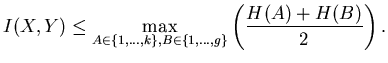 |
(8.5) |
Hence, we define
[0,1]-normalized mutual information-based quality as
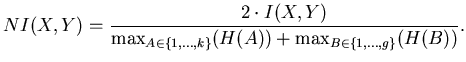 |
(8.6) |
Using
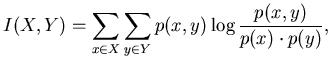 |
(8.7) |
and approximating probabilities with frequency counts delivers our
quality measure
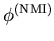 :
:
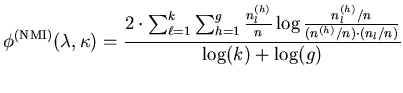 |
(8.8) |
Basic simplifications yield:
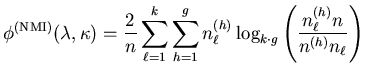 |
(8.9) |
This derivation is used to obtain
equations 4.25
and 5.2.
Instead of using the worst case upper bound for all possible labelings
and categorizations, one can assume that the categorization priors are
given. This allows a less aggressive denominator for
normalization: One can use the actual entropies 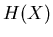 and
and 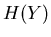 from the labelings
in equation B.4.
However, this results in a bias towards high
from the labelings
in equation B.4.
However, this results in a bias towards high  .
.
Another variant of normalization uses the actual entropies
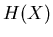 and
and 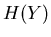 instead of
instead of
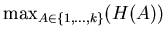 and
and
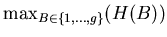 in
equation B.5.
For the results
presented in this dissertation, we will use the worst case
normalization (equation B.9).
in
equation B.5.
For the results
presented in this dissertation, we will use the worst case
normalization (equation B.9).




Next: Normalized Asymmetric Mutual Information
Up: Derivations
Previous: Derivations
Contents
Alexander Strehl
2002-05-03
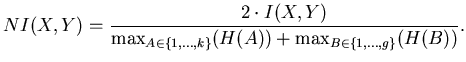
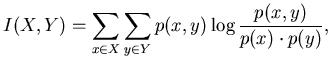
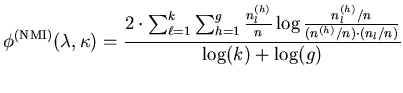
![]() and
and ![]() from the labelings
in equation B.4.
However, this results in a bias towards high
from the labelings
in equation B.4.
However, this results in a bias towards high ![]() .
.
![]() and
and ![]() instead of
instead of
![]() and
and
![]() in
equation B.5.
For the results
presented in this dissertation, we will use the worst case
normalization (equation B.9).
in
equation B.5.
For the results
presented in this dissertation, we will use the worst case
normalization (equation B.9).