



Next: Efficient Consensus Functions
Up: The Cluster Ensemble Problem
Previous: Illustrative Example
Contents
Objective Function for Cluster Ensembles
Given 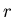 groupings with the
groupings with the 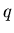 -th grouping
-th grouping
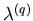 having
having 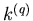 clusters,
a consensus function
clusters,
a consensus function 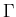 is defined as a
function
is defined as a
function
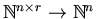 mapping a
set of clusterings to an integrated clustering:
mapping a
set of clusterings to an integrated clustering:
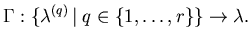 |
(5.1) |
We abbreviate the set of groupings
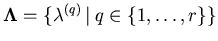 .
The optimal combined clustering should share the most information with
the original clusterings.
But how do we measure shared information between clusterings?
In information theory, mutual information is a symmetric measure to
quantify the statistical information shared between two distributions
[CT91].
Suppose there are two labelings
.
The optimal combined clustering should share the most information with
the original clusterings.
But how do we measure shared information between clusterings?
In information theory, mutual information is a symmetric measure to
quantify the statistical information shared between two distributions
[CT91].
Suppose there are two labelings
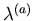 and
and
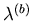 . Let there be
. Let there be 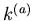 groups in
groups in
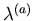 and
and 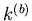 groups in
groups in
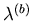 .
Let
.
Let 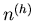 be the number of objects in cluster
be the number of objects in cluster
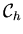 according to
according to
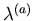 , and
, and 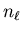 the number of
objects in cluster
the number of
objects in cluster
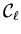 according to
according to
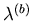 .
Let
.
Let
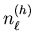 denote the number of objects that are in cluster
denote the number of objects that are in cluster
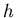 according to
according to
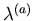 as well as in group
as well as in group 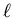 according to
according to
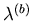 .
Then, a [0,1]-normalized mutual information criterion
.
Then, a [0,1]-normalized mutual information criterion
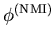 is computed as follows (see appendix
B.1 for details):
is computed as follows (see appendix
B.1 for details):
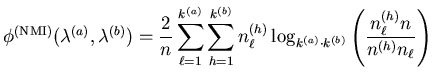 |
(5.2) |
Therefore, the Average Normalized Mutual Information (ANMI) between a
set of 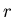 labelings,
labelings,
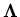 , and a labeling
, and a labeling
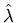 is defined as follows:
is defined as follows:
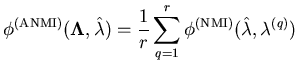 |
(5.3) |
We define the optimal combined clustering
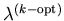 to be the one that has maximal
average mutual information with all individual labelings
to be the one that has maximal
average mutual information with all individual labelings
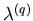 in
in
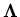 given that the number
of consensus clusters desired is
given that the number
of consensus clusters desired is  .
Our objective function
is average normalized mutual information
(ANMI, equation 5.3), and
.
Our objective function
is average normalized mutual information
(ANMI, equation 5.3), and
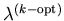 is defined as
is defined as
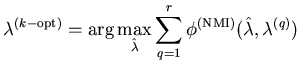 |
(5.4) |
where
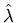 goes through all possible
goes through all possible
 -partitions [SG02a].
-partitions [SG02a].
There may be situations where not all labels are known for all
objects, i.e. there is missing data in the label vectors. For such
cases, the consensus clustering objective from equation
5.4 can be generalized by computing a
weighted average of the mutual information with the known labels, with the
weights proportional to the comprehensiveness of the labelings as
measured by the fraction of known labels. Let
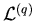 be
the set of object indices with known labels for the
be
the set of object indices with known labels for the 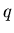 -th
labeling. Then, the generalized objective function becomes:
-th
labeling. Then, the generalized objective function becomes:
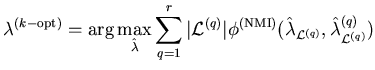 |
(5.5) |
For finite populations, the trivial solution is to exhaustively search
through all possible clusterings with  labels for the one with the
maximum ANMI. However, for
labels for the one with the
maximum ANMI. However, for 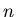 objects and
objects and  partitions there are
partitions there are
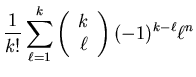 |
(5.6) |
possible clusterings, or approximately 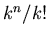 for
for 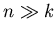 .
For example, there are 171,798,901 ways to form 4 groups of 16 objects.
For 8 groups of 32 objects this number grows to over
.
For example, there are 171,798,901 ways to form 4 groups of 16 objects.
For 8 groups of 32 objects this number grows to over
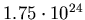 and for 16 groups of 64 objects to over
and for 16 groups of 64 objects to over
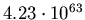 .
Clearly, this exponential growth in
.
Clearly, this exponential growth in 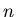 makes a full search
prohibitive. Having defined the objective, we now propose three
algorithms to find good heuristic solutions.
Note that greedy optimizations of the ANMI objective are difficult
since it is a hard
combinatorial problem. So our three proposed algorithms in this chapter
have been developed from intuitive ideas for maximizing the objective.
makes a full search
prohibitive. Having defined the objective, we now propose three
algorithms to find good heuristic solutions.
Note that greedy optimizations of the ANMI objective are difficult
since it is a hard
combinatorial problem. So our three proposed algorithms in this chapter
have been developed from intuitive ideas for maximizing the objective.




Next: Efficient Consensus Functions
Up: The Cluster Ensemble Problem
Previous: Illustrative Example
Contents
Alexander Strehl
2002-05-03
![]() groupings with the
groupings with the ![]() -th grouping
-th grouping
![]() having
having ![]() clusters,
a consensus function
clusters,
a consensus function ![]() is defined as a
function
is defined as a
function
![]() mapping a
set of clusterings to an integrated clustering:
mapping a
set of clusterings to an integrated clustering:
![]() be
the set of object indices with known labels for the
be
the set of object indices with known labels for the ![]() -th
labeling. Then, the generalized objective function becomes:
-th
labeling. Then, the generalized objective function becomes: