



Next: Objective Function for Cluster
Up: The Cluster Ensemble Problem
Previous: The Cluster Ensemble Problem
Contents
Illustrative Example
First, we will illustrate combining of clusterings using a simple
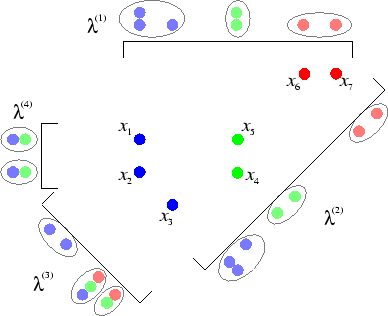
example. Consider the seven points on the 2D plane shown in figure
5.2. Four views are shown that project the data onto a
1D line. The square brackets denote the direction of projection as
well as the regions of observation.
Figure 5.2:
Illustration of multiple views generating different clusterings.
Seven objects in the 2D plane
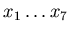 are projected onto
lines as illustrated by the square brackets. Only objects within the
square brackets are observed. The clusters in these views (shown as
bubbles) may deviate significantly from the original groups (shown by
colors) and vary tremendously amongst themselves. If the original 2D
and 1D features are unavailable and only the cluster
labels in the views are known, the input to the cluster ensemble is
the same as in
table
5.1.
are projected onto
lines as illustrated by the square brackets. Only objects within the
square brackets are observed. The clusters in these views (shown as
bubbles) may deviate significantly from the original groups (shown by
colors) and vary tremendously amongst themselves. If the original 2D
and 1D features are unavailable and only the cluster
labels in the views are known, the input to the cluster ensemble is
the same as in
table
5.1.
|
|
The scenario depicted in figure 5.2 is one out of many
that could have generated the following cluster ensemble problem.
Please note that there is no feature information available to the
cluster ensembles. The 2D spatial position of the seven data points is
not know in the cluster ensemble problem (and neither are the
projected 1D positions). The combining can only be based on the
cluster information.
Let the following label vectors specify four clusterings of
the same set of seven objects (see also table
5.1):
Inspection of the label vectors
reveals that clusterings 1
and 2 are logically identical.
Clustering 3 introduces some dispute about objects 3 and 5. Clustering
4 is quite inconsistent with all the other ones, has two groupings
instead of 3, and also contains missing data. Now let us look for a
good combined clustering with 3 clusters. Intuitively, a good combined clustering
should share as much information as possible with the given 4
labelings. Inspection suggests that a reasonable integrated
clustering is
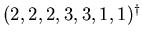 (or one of the 6
equivalent clusterings such as
(or one of the 6
equivalent clusterings such as
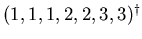 ). In
fact, after performing an exhaustive search over all 301 unique
clusterings of 7 elements into 3 groups, it can be shown that this
clustering shares the maximum information with the given 4 label
vectors (in terms that are more formally introduced in the next
subsection).
). In
fact, after performing an exhaustive search over all 301 unique
clusterings of 7 elements into 3 groups, it can be shown that this
clustering shares the maximum information with the given 4 label
vectors (in terms that are more formally introduced in the next
subsection).
This simple example illustrates some of the challenges. We have
already seen that the label vector is not unique. In fact, for each
unique clustering there are 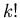 equivalent representations as integer
label vectors. However, only one representation satisfies the
following two constraints:
(i)
equivalent representations as integer
label vectors. However, only one representation satisfies the
following two constraints:
(i)
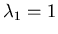 ;
(ii) for all
;
(ii) for all
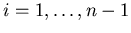 :
:
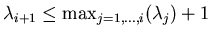 .
By allowing only representations that fulfill both constraints, the
integer vector representation can be forced to be unique.
Transforming the labels into this `canonical form' solves the
combining problem if all clusterings are actually the same. However,
if there is any discrepancy among labelings, one has to also deal with
a correspondence problem. In fact, there are
.
By allowing only representations that fulfill both constraints, the
integer vector representation can be forced to be unique.
Transforming the labels into this `canonical form' solves the
combining problem if all clusterings are actually the same. However,
if there is any discrepancy among labelings, one has to also deal with
a correspondence problem. In fact, there are
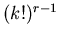 possible
association patterns.
In general, the number of clusters found as well as each cluster's
interpretation may vary tremendously among models.
possible
association patterns.
In general, the number of clusters found as well as each cluster's
interpretation may vary tremendously among models.




Next: Objective Function for Cluster
Up: The Cluster Ensemble Problem
Previous: The Cluster Ensemble Problem
Contents
Alexander Strehl
2002-05-03

![]() equivalent representations as integer
label vectors. However, only one representation satisfies the
following two constraints:
(i)
equivalent representations as integer
label vectors. However, only one representation satisfies the
following two constraints:
(i)
![]() ;
(ii) for all
;
(ii) for all
![]() :
:
![]() .
By allowing only representations that fulfill both constraints, the
integer vector representation can be forced to be unique.
Transforming the labels into this `canonical form' solves the
combining problem if all clusterings are actually the same. However,
if there is any discrepancy among labelings, one has to also deal with
a correspondence problem. In fact, there are
.
By allowing only representations that fulfill both constraints, the
integer vector representation can be forced to be unique.
Transforming the labels into this `canonical form' solves the
combining problem if all clusterings are actually the same. However,
if there is any discrepancy among labelings, one has to also deal with
a correspondence problem. In fact, there are
![]() possible
association patterns.
In general, the number of clusters found as well as each cluster's
interpretation may vary tremendously among models.
possible
association patterns.
In general, the number of clusters found as well as each cluster's
interpretation may vary tremendously among models.