



Next: Experiments on Text Documents
Up: Evaluation Methodology
Previous: Internal (model-based, unsupervised) Quality
Contents
External quality measures require an external grouping, for example as
indicated by category labels, that is assumed to be
`correct'. However, unlike in classification such ground truth is not
available to the clustering algorithm. This class of evaluation
measures can be used to compare start-to-end performance of any kind
of clustering regardless of the models or similarities used. However,
since clustering is an unsupervised problem, the performance cannot be
judged with the same certitude as for a classification problem. The
external categorization might not be optimal at all. For example, the
way web-pages are organized in the Yahoo! taxonomy is certainly not
the best structure possible. However, achieving a grouping similar to
the Yahoo! taxonomy is certainly indicative of successful clustering.
Given 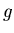 categories (or classes)
categories (or classes)
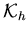 (
(
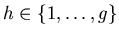 ), we denote the categorization label vector
), we denote the categorization label vector
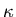 , where
, where
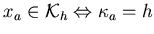 .
Let
.
Let 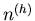 be the number of objects in category
be the number of objects in category
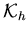 according to
according to
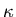 , and
, and 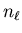 the number of
objects in cluster
the number of
objects in cluster
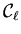 according to
according to
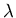 .
Let
.
Let
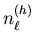 denote the number of objects that are in cluster
denote the number of objects that are in cluster
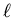 according to
according to
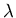 as well as in category
as well as in category 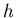 given by
given by
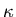 . There are several ways of comparing the
class labels with cluster labels:
. There are several ways of comparing the
class labels with cluster labels:
- Purity.
- Purity can be interpreted as classification accuracy under the
assumption that all objects of a cluster are classified to be members
of the dominant class for that cluster. For a single cluster
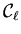 , purity is defined as the ratio of the number of
objects in the dominant category to the total number of objects:
, purity is defined as the ratio of the number of
objects in the dominant category to the total number of objects:
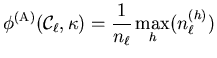 |
(4.17) |
To evaluate an entire clustering, one computes the average of the
cluster-wise purities weighted by cluster size:
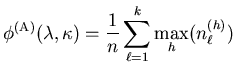 |
(4.18) |
- Entropy [CT91].
- Entropy is a more comprehensive measure than purity since rather than
just considering the number of objects `in' and `not in' the dominant
class, it takes the entire distribution into account. Since a cluster
with all objects from the same category has an entropy of 0, we define
entropy-based quality as 1 minus the
[0,1]-normalized entropy. We define entropy-based quality
for each cluster as:
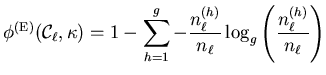 |
(4.19) |
And through weighted averaging, the total entropy quality measure falls
out to be:
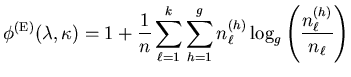 |
(4.20) |
Both, purity and entropy are biased to favor large number of clusters. In
fact, for both these criteria, the globally optimal value is trivially
reached when each cluster is a single object!
- Precision, recall &
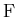 -measure [vR79].
-measure [vR79].
- Precision and recall are standard measures in the information
retrieval community. If a cluster is viewed as the results of a query for
a particular category, then precision is the fraction of correctly
retrieved objects:
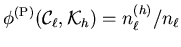 |
(4.21) |
Recall is the fraction of correctly retrieved objects out of all
matching objects in the database:
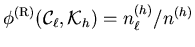 |
(4.22) |
The
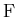 -measure combines precision and recall into a single number given
a weighting factor. The
-measure combines precision and recall into a single number given
a weighting factor. The
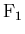 -measure combines precision and recall
with equal weights. The following equation gives the
-measure combines precision and recall
with equal weights. The following equation gives the
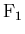 -measure
when querying for a particular category
-measure
when querying for a particular category
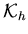
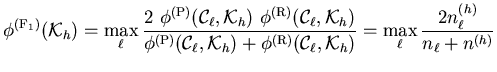 |
(4.23) |
Hence, for the entire clustering the total
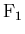 -measure is:
-measure is:
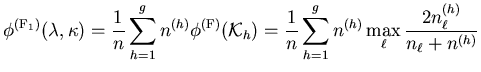 |
(4.24) |
Unlike
purity and entropy, the
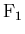 -measure is not biased towards a larger number of clusters. In fact, it favors coarser clusterings. Another
issue is that random clustering tends not to be evaluated at 0.
-measure is not biased towards a larger number of clusters. In fact, it favors coarser clusterings. Another
issue is that random clustering tends not to be evaluated at 0.
- Mutual information [CT91].
- The mutual information is the most theoretically well-founded among
the considered quality measures. It is unbiased and symmetric in terms
of
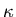 and
and
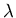 . We propose a
[0,1]-normalized mutual information-based quality criterion
. We propose a
[0,1]-normalized mutual information-based quality criterion
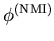 which can be computed as follows:
which can be computed as follows:
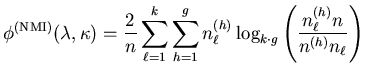 |
(4.25) |
A detailed derivation of this definition can be found in appendix
B.1. Mutual information does not suffer from the biases
like purity, entropy and the
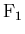 -measure. Singletons are not
evaluated as perfect. Random clustering has mutual information of 0 in
the limit. However, the best possible labeling evaluates to less than
1, unless classes are balanced.4.5Note that our normalization penalizes over-refinements unlike the
standard mutual information.4.6
-measure. Singletons are not
evaluated as perfect. Random clustering has mutual information of 0 in
the limit. However, the best possible labeling evaluates to less than
1, unless classes are balanced.4.5Note that our normalization penalizes over-refinements unlike the
standard mutual information.4.6
External criteria enable us to compare different clustering methods
fairly provided the external ground truth is of good quality. One
could argue against external criteria that clustering does not have to
perform as well as classification. However, in many cases clustering
is an interim step to better understand and characterize a complex
data-set before further analysis and modeling.
Normalized mutual information will be our preferred choice of
evaluation in the next section, because it is an unbiased measure for
the usefulness of the knowledge captured in the clustering in
predicting category labels.




Next: Experiments on Text Documents
Up: Evaluation Methodology
Previous: Internal (model-based, unsupervised) Quality
Contents
Alexander Strehl
2002-05-03
![]() categories (or classes)
categories (or classes)
![]() (
(
![]() ), we denote the categorization label vector
), we denote the categorization label vector
![]() , where
, where
![]() .
Let
.
Let ![]() be the number of objects in category
be the number of objects in category
![]() according to
according to
![]() , and
, and ![]() the number of
objects in cluster
the number of
objects in cluster
![]() according to
according to
![]() .
Let
.
Let
![]() denote the number of objects that are in cluster
denote the number of objects that are in cluster
![]() according to
according to
![]() as well as in category
as well as in category ![]() given by
given by
![]() . There are several ways of comparing the
class labels with cluster labels:
. There are several ways of comparing the
class labels with cluster labels: