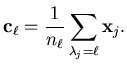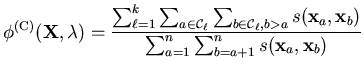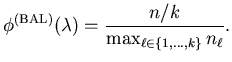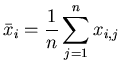Next: External (model-free, semi-supervised) Quality
Up: Evaluation Methodology
Previous: Evaluation Methodology
Contents
Internal quality measures, such as the sum of squared errors, have
traditionally been used extensively. Given an internal quality
measure, clustering can be posed as an optimization problem that is
typically solved via
greedy search. For example,  -means
has been shown to greedily optimize the sum of squared errors.
-means
has been shown to greedily optimize the sum of squared errors.
- Error (mean/sum-of-squared error, scatter matrices).
- The most popular cost function is the scatter of the points in each
cluster. Cost is measured as the mean square error of data points
compared to their respective cluster centroid.
The well known
 -means algorithm has been shown to heuristically
minimize the squared error objective. Let
-means algorithm has been shown to heuristically
minimize the squared error objective. Let 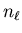 be the number of
objects in cluster
be the number of
objects in cluster
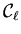 according to
according to
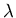 . Then, the cluster centroids are
. Then, the cluster centroids are
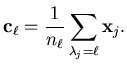 |
(4.9) |
The sum of squared errors
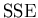 is
is
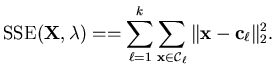 |
(4.10) |
Note that the
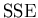 formulation can be extended to
other similarities by using
formulation can be extended to
other similarities by using
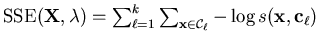 .
Since, we are interested in a quality measure ranging from 0 to 1,
where 1 indicates a perfect clustering, we define quality as
.
Since, we are interested in a quality measure ranging from 0 to 1,
where 1 indicates a perfect clustering, we define quality as
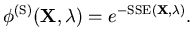 |
(4.11) |
This objective can also be viewed from a probability density
estimation perspective using EM [DLR77]. Assuming the data is
generated by a mixture of multi-variate Gaussians with identical,
diagonal covariance matrices, the
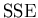 objective is
equivalent to the maximizing the likelihood of observing the
data by adjusting the centers and minimizing weights of the
Gaussian mixture.
objective is
equivalent to the maximizing the likelihood of observing the
data by adjusting the centers and minimizing weights of the
Gaussian mixture.
- Edge cut.
- When clustering is posed as a graph partitioning problem, the
objective is to minimize edge cut. Formulated as a [0,1]-quality
maximization problem, the objective is the ratio of remaining
edge weights to total pre-cut edge weights:
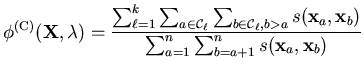 |
(4.12) |
Note that this quality measure can be trivially maximized when there
are no restrictions on the sizes of clusters. In other words, edge cut
quality evaluation is only fair when the compared clusterings are
well-balanced. Let us define the balance of a clustering
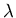 as
as
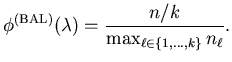 |
(4.13) |
A balance of 1 indicates that all clusters have the same size. In
certain applications, balanced clusters are desirable because each
cluster represents an equally important share of the data. Balancing
has application driven advantages e.g., for distribution, navigation,
summarization of the clustered objects. In chapter 3, retail
customer clusters are balanced so they represent an equal share of
revenue. Balanced clustering for browsing text documents have also
been proposed [BG02].
However, some natural classes may not be of equal size, so relaxed
balancing may become necessary.
A middle ground between no constraints on balancing (e.g.,
 -means) and tight balancing (e.g., graph partitioning) can be
achieved by over-clustering using a balanced algorithm and then merging
clusters subsequently [KHK99].
-means) and tight balancing (e.g., graph partitioning) can be
achieved by over-clustering using a balanced algorithm and then merging
clusters subsequently [KHK99].
- Category Utility [GC85,Fis87a].
- The category utility function measures quality as the increase in
predictability of attributes given a clustering. Category utility is
defined as the increase in the expected number of attribute
values that can be correctly guessed given a partitioning, over
the expected number of correct guesses with no such knowledge. A
weighted average over categories allows comparison of different sized
partitions. For binary features (i.e., attributes) the probability of
the
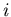 -th attribute to be 1 is the mean of the
-th attribute to be 1 is the mean of the 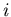 -th row of the data
matrix
-th row of the data
matrix
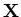 :
:
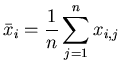 |
(4.14) |
The conditional probability of the 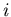 -th attribute to be 1 given
that the data point is in cluster
-th attribute to be 1 given
that the data point is in cluster 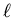 is
is
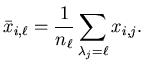 |
(4.15) |
Hence, category utility can be written as
![$\displaystyle \phi^{(\mathrm{CU})} ( \mathbf{X}, \lambda ) = \frac{4}{d} \sum_{...
...- \left( \sum_{i=1}^{d} \left( \bar{x}_i^2 - \bar{x}_i \right) \right) \right].$](img353.png) |
(4.16) |
Note that our definition divides the standard category by 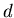 so that
so that
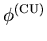 never exceeds 1.
Recently, it has been shown that category utility is related to
squared error criterion for a particular standard encoding
[Mir01].
Category utility is defined to maximize predictability of attributes
for a clustering. This limits the scope of this quality measure to
low-dimensional clustering problems (preferably with each dimension
being a categorical variable with small cardinality). In
high-dimensional problems, such as text clustering, the objective is
not to be able to predict the appearance of any possible word in
a document from a particular cluster. In fact, there might be more
unique words / terms / phrases than documents in a small data-set. In
preliminary experiments, category utility did not succeed in
differentiating among the compared approaches (including random
partitioning).
never exceeds 1.
Recently, it has been shown that category utility is related to
squared error criterion for a particular standard encoding
[Mir01].
Category utility is defined to maximize predictability of attributes
for a clustering. This limits the scope of this quality measure to
low-dimensional clustering problems (preferably with each dimension
being a categorical variable with small cardinality). In
high-dimensional problems, such as text clustering, the objective is
not to be able to predict the appearance of any possible word in
a document from a particular cluster. In fact, there might be more
unique words / terms / phrases than documents in a small data-set. In
preliminary experiments, category utility did not succeed in
differentiating among the compared approaches (including random
partitioning).
Using internal quality measures, fair comparisons can only be made
amongst clusterings with the same choices of vector representation and
similarity / distance measure. E.g., using edge-cut in cosine-based
similarity would not be meaningful for an evaluation of Euclidean
 -means. So, in many applications a consensus on the internal
quality measure for clustering is not found. However, in situations
where the pages are categorized (labelled) by an external source,
there is a plausible way out!
-means. So, in many applications a consensus on the internal
quality measure for clustering is not found. However, in situations
where the pages are categorized (labelled) by an external source,
there is a plausible way out!




Next: External (model-free, semi-supervised) Quality
Up: Evaluation Methodology
Previous: Evaluation Methodology
Contents
Alexander Strehl
2002-05-03
![]() -means
has been shown to greedily optimize the sum of squared errors.
-means
has been shown to greedily optimize the sum of squared errors.