Clearly, if clusters are to be meaningful, the similarity measure should be invariant to transformations natural to the problem domain. Also, normalization may strongly affect clustering in a positive or negative way. The features have to be chosen carefully to be on comparable scales and similarity has to reflect the underlying semantics for the given task.
Euclidean similarity is translation invariant but scale sensitive while
cosine is translation sensitive but scale invariant. The extended
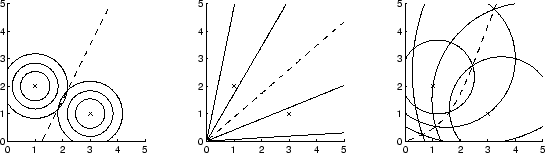
Jaccard has aspects of both properties as illustrated in figure
4.1. Iso-similarity lines at ![]() , 0.5 and
0.75 for points
, 0.5 and
0.75 for points
![]() and
and
![]() are shown for Euclidean, cosine, and the extended
Jaccard. For cosine similarity only the 4 (out of 12) lines that are
in the positive quadrant are plotted: The two lines in the lower right
part are one of two lines from
are shown for Euclidean, cosine, and the extended
Jaccard. For cosine similarity only the 4 (out of 12) lines that are
in the positive quadrant are plotted: The two lines in the lower right
part are one of two lines from
![]() at 0.5 and 0.75.
The two lines in the upper left are for
at 0.5 and 0.75.
The two lines in the upper left are for
![]() at
at ![]() and
0.75. The dashed line marks the locus of equal similarity to
and
0.75. The dashed line marks the locus of equal similarity to
![]() and
and
![]() which always passes through the
origin for cosine and extended Jaccard similarity.
which always passes through the
origin for cosine and extended Jaccard similarity.
Using Euclidean similarity
![]() , iso-similarities are
concentric hyperspheres around the considered point. Due to the
finite range of similarity, the radius decreases hyperbolically as
, iso-similarities are
concentric hyperspheres around the considered point. Due to the
finite range of similarity, the radius decreases hyperbolically as
![]() increases linearly. The radius does not depend on
the center-point. The only location with similarity of 1 is the
considered point itself and all finite locations have a similarity
greater than 0. This last property tends to generate non-sparse
similarity matrices. Using the cosine measure
increases linearly. The radius does not depend on
the center-point. The only location with similarity of 1 is the
considered point itself and all finite locations have a similarity
greater than 0. This last property tends to generate non-sparse
similarity matrices. Using the cosine measure
![]() renders the iso-similarities to be hypercones all having their apex
at the origin and axis aligned with the considered point. Locations
with similarity 1 are on the 1-dimensional sub-space defined by
this axis. The locus of points with similarity 0 is the hyperplane
through the origin and perpendicular to this axis. For the extended
Jaccard similarity
renders the iso-similarities to be hypercones all having their apex
at the origin and axis aligned with the considered point. Locations
with similarity 1 are on the 1-dimensional sub-space defined by
this axis. The locus of points with similarity 0 is the hyperplane
through the origin and perpendicular to this axis. For the extended
Jaccard similarity
![]() , the iso-similarities are
non-concentric hyperspheres. The only location with similarity 1 is
the point itself. The hypersphere radius increases with the the
distance of the considered point from the origin so that longer
vectors turn out to be more tolerant in terms of similarity than
smaller vectors. Sphere radius also increases with similarity and as
, the iso-similarities are
non-concentric hyperspheres. The only location with similarity 1 is
the point itself. The hypersphere radius increases with the the
distance of the considered point from the origin so that longer
vectors turn out to be more tolerant in terms of similarity than
smaller vectors. Sphere radius also increases with similarity and as
![]() approaches 0 the radius becomes infinite
rendering the sphere to the same hyperplane as obtained for cosine
similarity. Thus, for
approaches 0 the radius becomes infinite
rendering the sphere to the same hyperplane as obtained for cosine
similarity. Thus, for
![]() , extended
Jaccard behaves like the cosine measure, and for
, extended
Jaccard behaves like the cosine measure, and for
![]() , it behaves like the Euclidean distance.
, it behaves like the Euclidean distance.
|
|
In traditional Euclidean ![]() -means clustering the optimal cluster
representative
-means clustering the optimal cluster
representative
![]() minimizes the sum of squared error
criterion, i.e.,
minimizes the sum of squared error
criterion, i.e.,
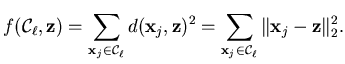 |
(4.6) |
 |
(4.7) |
To illustrate the values of the
evaluation function
![]() are used to shade the background in figure 4.2. The
maximum likelihood representative of
are used to shade the background in figure 4.2. The
maximum likelihood representative of
![]() and
and
![]() is marked with a
is marked with a ![]() in figure 4.2. For cosine
similarity all points on the equi-similarity are optimal
representatives.
In a maximum likelihood interpretation, we constructed the distance
similarity transformation such that
in figure 4.2. For cosine
similarity all points on the equi-similarity are optimal
representatives.
In a maximum likelihood interpretation, we constructed the distance
similarity transformation such that
![]() .
Consequently, we can use the dual interpretations of probabilities in
similarity space and errors in distance space.
.
Consequently, we can use the dual interpretations of probabilities in
similarity space and errors in distance space.