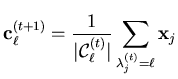


Next: Robust -medoids
Up: Clustering Algorithms
Previous: Clustering Algorithms
Contents
The 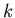 -means algorithm is a very simple and very powerful iterative
technique to partition a data-set into
-means algorithm is a very simple and very powerful iterative
technique to partition a data-set into 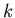 disjoint clusters, where
the value
disjoint clusters, where
the value 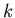 has to be pre-determined [DH73,Har75]. A
generalized, similarity-based description of the algorithm can be
given as follows:
has to be pre-determined [DH73,Har75]. A
generalized, similarity-based description of the algorithm can be
given as follows:
- Start at
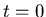 with
with 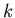 randomly selected objects as
the cluster centers
randomly selected objects as
the cluster centers
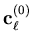 ,
,
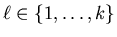 .
.
- Assign each object
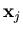 to the cluster center with maximum
similarity:
to the cluster center with maximum
similarity:
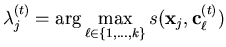 |
(2.1) |
- Update all
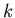 cluster means:
cluster means:
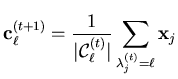 |
(2.2) |
- If any
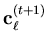 differs from
differs from
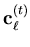 go to step 2 with
go to step 2 with
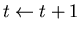 unless termination criteria (such as exceeding the maximum number of
iterations) are met.
unless termination criteria (such as exceeding the maximum number of
iterations) are met.
When similarity is based on a strictly monotonic decreasing mapping of
Euclidean distances, 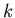 -means greedily minimizes the sum of squared
distances of the samples
-means greedily minimizes the sum of squared
distances of the samples
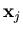 to the closest cluster
centroid
to the closest cluster
centroid
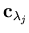 as given by equation
2.3.
as given by equation
2.3.
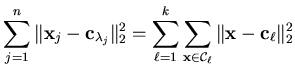 |
(2.3) |



Next: Robust -medoids
Up: Clustering Algorithms
Previous: Clustering Algorithms
Contents
Alexander Strehl
2002-05-03
![]() -means algorithm is a very simple and very powerful iterative
technique to partition a data-set into
-means algorithm is a very simple and very powerful iterative
technique to partition a data-set into ![]() disjoint clusters, where
the value
disjoint clusters, where
the value ![]() has to be pre-determined [DH73,Har75]. A
generalized, similarity-based description of the algorithm can be
given as follows:
has to be pre-determined [DH73,Har75]. A
generalized, similarity-based description of the algorithm can be
given as follows: