The objects to be clustered can be viewed as a set of vertices
![]() . Two web-pages
. Two web-pages
![]() and
and
![]() (or
vertices
(or
vertices ![]() and
and ![]() ) are connected with an undirected edge of
positive weight
) are connected with an undirected edge of
positive weight
![]() , or
, or
![]() . The cardinality
of the set of edges
. The cardinality
of the set of edges
![]() equals the number of non-zero similarities between all pairs of samples. A set of edges
whose removal partitions a graph
equals the number of non-zero similarities between all pairs of samples. A set of edges
whose removal partitions a graph
![]() into
into ![]() pair-wise disjoint
sub-graphs
pair-wise disjoint
sub-graphs
![]() , is called an edge
separator. Our objective is to find such a separator with a minimum
sum of edge weights. While striving for the minimum cut objective,
the number of objects in each cluster has to be kept approximately
equal. In this particular case of balancing, the problem is NP-hard
and known as graph partitioning.
, is called an edge
separator. Our objective is to find such a separator with a minimum
sum of edge weights. While striving for the minimum cut objective,
the number of objects in each cluster has to be kept approximately
equal. In this particular case of balancing, the problem is NP-hard
and known as graph partitioning.
Balanced clusters are desirable because each cluster represents an
equally important share of the data. However, some natural classes
may not be equal size. By using a higher number of clusters we can
account for multi-modal classes (e.g., XOR-problem) and clusters can
be merged at a latter stage. The most expensive step in this
![]() technique is the computation of the
technique is the computation of the
![]() similarity
matrix. In document clustering, sparsity can be induced by looking
only at the
similarity
matrix. In document clustering, sparsity can be induced by looking
only at the ![]() strongest edges or at the subgraph induced by pruning
all edges except the
strongest edges or at the subgraph induced by pruning
all edges except the ![]() nearest-neighbors for each vertex. Sparsity
makes this approach feasible for large data-sets.
nearest-neighbors for each vertex. Sparsity
makes this approach feasible for large data-sets.
The Kernighan-Lin (KL) algorithm has been a very successful ![]() algorithm for graph partitioning [KL70]. The KL is based on
iteratively conducting best sequences of swaps involving all vertices.
In an improved implementation by Fiduccia and Mattheyses
[FM82], the complexity was of the KL algorithm was reduced to
algorithm for graph partitioning [KL70]. The KL is based on
iteratively conducting best sequences of swaps involving all vertices.
In an improved implementation by Fiduccia and Mattheyses
[FM82], the complexity was of the KL algorithm was reduced to
![]() .
.
In spectral bisection [HL95,PSL90] the partitioning
problem is reduced to finding the second least dominant eigenvector of
the Laplacian matrix ![]() . Consider the incidence matrix
. Consider the incidence matrix
![]() whose entries are defined as follows:
whose entries are defined as follows:
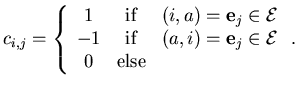 |
(2.16) |
| (2.17) |
Currently, the best available algorithms use the KL-algorithm or spectral bisection in a multi-level framework which has three stages:
A hypergraph is a graph whose edges can connect more than two
vertices (hyperedges). The clustering problem is then formulated as a
finding the minimum-cut of a hypergraph. A minimum-cut is the removal
of the set of hyperedges (with minimum edge weight) that separates
the hypergraph into ![]() unconnected components. Again, an object
unconnected components. Again, an object
![]() maps to a vertex
maps to a vertex ![]() . Each feature maps to a
hyperedge connecting all vertices with a non-zero value for this
particular feature, so
. Each feature maps to a
hyperedge connecting all vertices with a non-zero value for this
particular feature, so
![]() . The minimum-cut of this
hypergraph into
. The minimum-cut of this
hypergraph into ![]() unconnected components gives the desired
clustering. Hypergraphs are often used in VLSI design. An
application to association rule hypergraph clustering can be
found in [BGG$^+$99].
unconnected components gives the desired
clustering. Hypergraphs are often used in VLSI design. An
application to association rule hypergraph clustering can be
found in [BGG$^+$99].
A variety of packages for graph partitioning is available. A Matlab kit for geometric mesh partitioning (requires coordinate information for vertices) [GMT95] and spectral bi-section [PSL90] by John R. Gilbert and Shang-Hua Teng is available from Xerox. Currently, the most popular programs for graph partitioning are CHACO (available from Bruce Hendrickson at Los Alamos National Labs) [HL94] and METIS (George Karypis, University of Minnesota) [KK98a,KK98b]. Both implement the currently fastest available algorithm, a multi-level version of Kernighan-Lin [KL70,FM82]. A popular package for hypergraph partitioning is HMETIS (George Karypis, University of Minnesota) [KAKS97].