



Next: Visualization
Up: Background and Related Work
Previous: Graph and Hypergraph Partitioning
Contents
Scalability
High-dimensional data is often very sparse, e.g. most entries in the
data matrix are zero. Using this sparsity in efficient data structures
and algorithms can reduce temporal and storage complexity by several
orders of magnitude. Scalability can be investigated in terms of the
number of objects 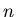 and the number of dimensions
and the number of dimensions 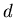 . Traditionally,
scaling to large
. Traditionally,
scaling to large 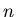 has been considered more. In this dissertation,
we focus on applications with large
has been considered more. In this dissertation,
we focus on applications with large 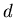 . For scaling to large
. For scaling to large 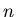 ,
there are four main ways of reducing complexity in order to scale
clustering algorithms:
,
there are four main ways of reducing complexity in order to scale
clustering algorithms:
- Sampling.
- Sample the data, cluster the sample points
and then use a quick heuristic to allocate the non-sampled points to
the initial clusters. This approach will yield a faster algorithm at
the cost of some possible loss in quality, and is employed, for
example in the Buckshot algorithm for the Scatter/Gather approach to
iterative clustering for interactive browsing [CKPT92]. If the
sample is
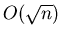 , and `nearest cluster center' is used to
allocate the remaining points, one obtains an
, and `nearest cluster center' is used to
allocate the remaining points, one obtains an 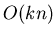 algorithm. Also
related are randomized approaches that can partition a set of points
into two clusters of comparable size in sublinear time, producing a
(1+
algorithm. Also
related are randomized approaches that can partition a set of points
into two clusters of comparable size in sublinear time, producing a
(1+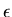 ) solution with high probability [Ind99]. We
shall show later that since OPOSSUM is based on balanced
clusters, sampling is a good choice since one can ensure with high
probability that each cluster is represented in the sample without
needing a large sample size.
) solution with high probability [Ind99]. We
shall show later that since OPOSSUM is based on balanced
clusters, sampling is a good choice since one can ensure with high
probability that each cluster is represented in the sample without
needing a large sample size.
- Sequential building.
- Construct a `core' clustering using a small number of elements, and
then sequentially scan the data to allocate the remaining inputs,
creating new clusters (and optionally adjusting existing centers) as
needed. Such an approach is seen e.g., in BIRCH [ZRL97]. This
style compromises balancing to some extent, and the threshold
determining when a new cluster is formed has to be experimented with
to bring the number of clusters obtained to the desired range. A
version of this approach for graph partitioning using a corrupted
clique model was proposed by
[BDSY99] and applied to clustering gene expressions. This can be
readily used for OPOSSUM as well. Sequential building is
specially popular for out-of-core methods, the idea being to scan the
database once to form a summarized model (for instance, the size, sum
and sum-squared values of each cluster [BFR98]) in main memory.
Subsequent refinement based on summarized information is then
restricted to main memory operations without resorting to further disk
scans.
- Representatives.
- Compare with representatives rather than
with all points. Using
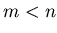 representatives reduces the number of
similarities to be considered from
representatives reduces the number of
similarities to be considered from 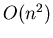 to
to 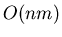 . For example,
in
. For example,
in  -means, the current cluster means are used as
representatives. Since points do not have to compared to all others
but only to a few centroids (the current means), scalability is
considerably improved. The results, however, become sensitive to the
initial selection of representatives. Also, representatives might
have to be updated resulting in an iterative algorithm.
-means, the current cluster means are used as
representatives. Since points do not have to compared to all others
but only to a few centroids (the current means), scalability is
considerably improved. The results, however, become sensitive to the
initial selection of representatives. Also, representatives might
have to be updated resulting in an iterative algorithm.
- Pre-segmentation.
- Apply prior domain knowledge to pre-segment
the data, e.g. using indices or other `partitionings' of the input
space. Pre-segmentations can be coarser (e.g., to reduce pairwise
comparisons by only comparing within segments) or finer (e.g., to
summarize points as a pre-processing step as in BIRCH) than the final
clustering. As mentioned earlier, this becomes increasingly
problematic as the dimensionality of the input space increases to the
hundreds or beyond, where the suitable segments may be difficult to
estimate, pre-determine, or populate.
All these approaches are somewhat orthogonal to the main clustering
routine in that they can be applied in conjunction with most core
clustering routines to save computation, at the cost of some loss in
quality.




Next: Visualization
Up: Background and Related Work
Previous: Graph and Hypergraph Partitioning
Contents
Alexander Strehl
2002-05-03
![]() and the number of dimensions
and the number of dimensions ![]() . Traditionally,
scaling to large
. Traditionally,
scaling to large ![]() has been considered more. In this dissertation,
we focus on applications with large
has been considered more. In this dissertation,
we focus on applications with large ![]() . For scaling to large
. For scaling to large ![]() ,
there are four main ways of reducing complexity in order to scale
clustering algorithms:
,
there are four main ways of reducing complexity in order to scale
clustering algorithms: