



Next: Ensembles and Knowledge Reuse
Up: Background and Related Work
Previous: Scalability
Contents
Visualization
Visualization of high-dimensional data clusters can be largely divided
into four popular approaches:
- Dimensionality reduction by selection of 2 or 3 dimensions,
or, more generally, projecting the data down to 2 or 3 dimensions.
Often these dimensions correspond to principal components or a
scalable approximation thereof (e.g., FASTMAP
[FL95]). Chen, for example, creates a browsable
2-dimensional space of authors through co-citations [Che99].
Another noteworthy method is CViz [DMS98], which projects
onto the plane that passes through three selected cluster centroids to
yield a `discrimination optimal' 2-dimensional projection. These
projections are useful for a medium number of dimensions, i.e., if
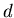 is not too large (
is not too large ( 100).2.3Nonlinear projections have also been studied [CG01].
Recreating a 2- or 3-dimensional space from a similarity graph can
also be done through multi-dimensional scaling [Tor52].
100).2.3Nonlinear projections have also been studied [CG01].
Recreating a 2- or 3-dimensional space from a similarity graph can
also be done through multi-dimensional scaling [Tor52].
- Parallel axis plots show each object as a line along
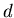 parallel axis. However, this technique is rendered ineffective if the
number of dimensions
parallel axis. However, this technique is rendered ineffective if the
number of dimensions 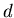 or the number of objects gets too high.
or the number of objects gets too high.
- Kohonen's Self Organizing Map (SOM) [Koh90]
provides an innovative and powerful way of clustering while enforcing
constraints on a logical topology imposed on the cluster centers. If
this topology is 2-dimensional, one can readily "visualize" the
clustering of data. Essentially a 2-dimensional manifold is mapped
onto the (typically higher dimensional) feature space, trying to
approximate data density while maintaining topological constraints.
Since the mapping is not bijective, the quality can degrade very
rapidly with increasing dimensionality of feature space, unless the
data is largely confined to a much lower order manifold within this
space [CG01]. Multi-Dimensional Scaling (MDS) and associated
methods also face similar issues.
- Visualization can also be done by showing the data matrix as
an image by converting entries to brightness values. The ordering of
data points for visualization has previously been used in conjunction
with clustering in different contexts. For example, in OPTICS
[ABKS99] instead of producing an explicit clustering, an
augmented ordering of the database is produced. Subsequently, this
ordering is used to display various metrics such as reachability
values.
In cluster analysis of genome data [ESBB98] re-ordering the
primary data matrix and representing it graphically has been explored.
This visualization takes place in the primary data space rather than
in the relationship-space.
Sparse primary data matrix reorderings have also been considered for
browsing hypertext [BHR96].
A useful survey of visualization methods for data mining in general
can be found in [KK96]. The popular books by E. Tufte
[Tuf83] on visualizing information are also recommended.




Next: Ensembles and Knowledge Reuse
Up: Background and Related Work
Previous: Scalability
Contents
Alexander Strehl
2002-05-03