Next: Curse of Dimensionality
Up: Challenges
Previous: Challenges
Contents
The Problem of Scale
Most clustering algorithms assume the number of clusters to be known
a priori. The desired granularity is generally determined by
external, problem specific criteria. For example, such a criterion
might be the user's willingness to deal with complexity and
information overload. This issue of scale remains mostly unsolved
although various promising attempts such as Occam's razor, minimum
description length, category utility, etc. have been made.
Finding the `right' number of clusters,  , for a data-set is a
difficult, and often ill-posed, problem. Gelman in [GCSR95] on
page 424 says in a mixture modeling context: ``One viewpoint is that
the problem of finding the best number of clusters is fundamentally
ill-defined and best avoided.'' Let us illustrate the problem by a
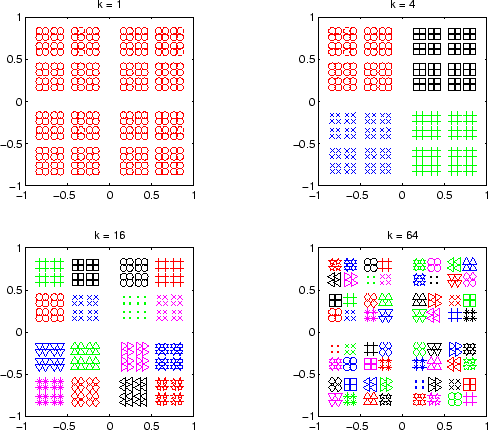
data-set where points are arranged in a grid-like pattern on the 2D
plane (figure 2.1). The points are arranged in four
squares such that when `zooming in' the same square structure exists
but on a lower scale. When asking what is the number of clusters for
that data-set, there are at least 3 good answers possible, namely 4,
16, and 64. Depending on the desired resolution the `right' number
of clusters changes. In general, there are multiple good
, for a data-set is a
difficult, and often ill-posed, problem. Gelman in [GCSR95] on
page 424 says in a mixture modeling context: ``One viewpoint is that
the problem of finding the best number of clusters is fundamentally
ill-defined and best avoided.'' Let us illustrate the problem by a
data-set where points are arranged in a grid-like pattern on the 2D
plane (figure 2.1). The points are arranged in four
squares such that when `zooming in' the same square structure exists
but on a lower scale. When asking what is the number of clusters for
that data-set, there are at least 3 good answers possible, namely 4,
16, and 64. Depending on the desired resolution the `right' number
of clusters changes. In general, there are multiple good  's for any
given data. However, a certain number of clusters might be more stable
than others. In the example shown in figure 2.1, five
clusters is probably not a better choice than four.
's for any
given data. However, a certain number of clusters might be more stable
than others. In the example shown in figure 2.1, five
clusters is probably not a better choice than four.
Since there seems to be no definite answer to how many clusters are
in a data-set, a user-defined criterion for the resolution has to be
given instead. In the general case, the number of clusters is
assumed to be known. Alternatively, one might want to reformulate the
specification of scale through an upper bound of acceptable error
(which has to be suitably defined) or some other criterion.
Figure 2.1:
Example for the problem of scale.
Four examplary clusterings are shown for the 2-dimensional RECSQUARE data-set. 4, 16, and 64 are `equally good' choices for
the number of clusters  .
.
|
|
Many heuristics for finding the right number of clusters have been
proposed. Occam's razor states that the simplest hypothesis that fits
the data is the best [BEHW87,Mit97]. Generally, as the model
complexity grows the fit improves. However, over-learning with a loss
of generalization may occur. In probabilistic clustering,
likelihood-ratios, 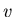 -fold-cross-validation, penalized likelihoods
(e.g., Bayesian information criterion), and Bayesian techniques
(AUTOCLASS) are popular [Smy96,MC85]:
-fold-cross-validation, penalized likelihoods
(e.g., Bayesian information criterion), and Bayesian techniques
(AUTOCLASS) are popular [Smy96,MC85]:
- Cross-validation.
- A recent Monte Carlo cross-validation based approach [Mil81]
which minimizes the Kullback-Leibler information distance to find the
right number of clusters can be found in
[Smy96].
- Category Utility.
- In machine learning, category utility
[GC85,Fis87a] has been used to asses the quality of a
clustering for a particular
 . Category utility is defined as the
increase in the expected number of attribute values
. Category utility is defined as the
increase in the expected number of attribute values 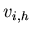 (the
(the 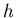 -th discrete level of feature
-th discrete level of feature 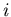 ) that can be correctly
guessed, given a partitioning
) that can be correctly
guessed, given a partitioning
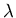 over the
expected number of correct guesses with no such knowledge. A weighted
average over categories allows comparison of different size
partitions.
over the
expected number of correct guesses with no such knowledge. A weighted
average over categories allows comparison of different size
partitions.
- Bayesian Solution.
- In the full Bayesian solution the posterior probabilities of all
values of
 are computed from the data and priors for the data and
are computed from the data and priors for the data and
 itself. AUTOCLASS [CS96] uses this approach
with some approximations to avoid computational issues with the
complexity of this approach. The complexity makes this approach
infeasible for very high-dimensional data.
itself. AUTOCLASS [CS96] uses this approach
with some approximations to avoid computational issues with the
complexity of this approach. The complexity makes this approach
infeasible for very high-dimensional data.
- Regularization.
- A feasible approach for high-dimensional data mining is a
regularization-based approach. A penalty term is introduced to
discourage a high number of parameters. Variations of this theme
include penalized likelihoods, such as the Bayesian Information
Criterion (BIC), and coding-based criteria, such as Minimum
Description Length (MDL).




Next: Curse of Dimensionality
Up: Challenges
Previous: Challenges
Contents
Alexander Strehl
2002-05-03
![]() , for a data-set is a
difficult, and often ill-posed, problem. Gelman in [GCSR95] on
page 424 says in a mixture modeling context: ``One viewpoint is that
the problem of finding the best number of clusters is fundamentally
ill-defined and best avoided.'' Let us illustrate the problem by a
data-set where points are arranged in a grid-like pattern on the 2D
plane (figure 2.1). The points are arranged in four
squares such that when `zooming in' the same square structure exists
but on a lower scale. When asking what is the number of clusters for
that data-set, there are at least 3 good answers possible, namely 4,
16, and 64. Depending on the desired resolution the `right' number
of clusters changes. In general, there are multiple good
, for a data-set is a
difficult, and often ill-posed, problem. Gelman in [GCSR95] on
page 424 says in a mixture modeling context: ``One viewpoint is that
the problem of finding the best number of clusters is fundamentally
ill-defined and best avoided.'' Let us illustrate the problem by a
data-set where points are arranged in a grid-like pattern on the 2D
plane (figure 2.1). The points are arranged in four
squares such that when `zooming in' the same square structure exists
but on a lower scale. When asking what is the number of clusters for
that data-set, there are at least 3 good answers possible, namely 4,
16, and 64. Depending on the desired resolution the `right' number
of clusters changes. In general, there are multiple good ![]() 's for any
given data. However, a certain number of clusters might be more stable
than others. In the example shown in figure 2.1, five
clusters is probably not a better choice than four.
's for any
given data. However, a certain number of clusters might be more stable
than others. In the example shown in figure 2.1, five
clusters is probably not a better choice than four.