Next: Clustering Objectives
Up: Challenges
Previous: The Problem of Scale
Contents
Curse of Dimensionality
When dealing with very high-dimensional data, one is faced with the
`curse of dimensionality' [Fri94] and the associated sparsity
issues. Essentially the amount of data to sustain a given spatial
density increases exponentially with the dimensionality of the input
space, or alternatively, the sparsity increases exponentially given a
constant amount of data, with points tending to become equidistant
from one another. In general, this will adversely impact any method
based on spatial density, unless the data follows certain simple
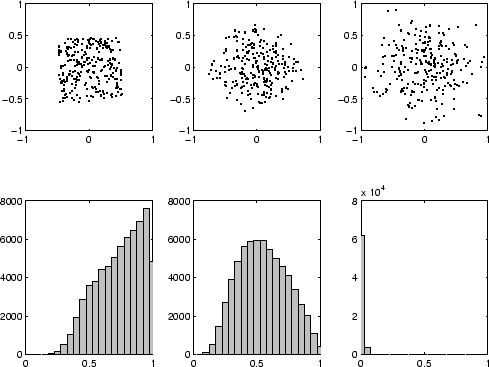
distributions. Figure 2.2 gives a simple
illustration of the curse of dimensionality.
Figure 2.2:
Curse of dimensionality illustrated with 256 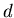 -dimensional
points from a [0,1] uniform distribution with
-dimensional
points from a [0,1] uniform distribution with 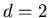 (left), 4
(middle) and 32 (right). The top row shows the results of the 2D
Principal Components Analysis (PCA). The bottom row shows how
similarity (as a monotonically decreasing function of Euclidean
distance) is distributed.
As
(left), 4
(middle) and 32 (right). The top row shows the results of the 2D
Principal Components Analysis (PCA). The bottom row shows how
similarity (as a monotonically decreasing function of Euclidean
distance) is distributed.
As 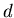 increases, projections approach Gaussian distributions. Also,
an average pair of points' similarity decreases rapidly and
similarities become approximately equal for most pairs with increasing
increases, projections approach Gaussian distributions. Also,
an average pair of points' similarity decreases rapidly and
similarities become approximately equal for most pairs with increasing
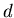 .
.
|
|




Next: Clustering Objectives
Up: Challenges
Previous: The Problem of Scale
Contents
Alexander Strehl
2002-05-03