



Next: Domain Specific Features and
Up: Relationship-based Clustering and Visualization
Previous: Relationship-based Clustering and Visualization
Contents
Motivation
Knowledge discovery in databases often requires clustering the data
into a number of distinct segments or groups in an effective and
efficient manner. Good clusters show high similarity within a group
and low similarity between any two different groups. Besides
producing good clusters, certain clustering methods provide additional
useful benefits. For example, Kohonen's Self-Organizing feature Map
(SOM) [Koh90] imposes a logical, `topographic' ordering
on the cluster centers such that centers that are nearby in the
logical ordering represent nearby clusters in the feature space. A
popular choice for the logical ordering is a two-dimensional lattice
which allows all the data points to be projected onto a
two-dimensional plane for convenient visualization [Hay99].
While clustering is a classical and well studied area, it turns out
that several data mining applications pose some unique challenges that
severely test traditional techniques for clustering and cluster
visualization. For example, consider the following two
applications:
- Grouping customers based on buying behavior to
provide useful marketing decision support knowledge; especially in
e-business applications where electronically observed behavioral data
is readily available. Customer clusters can be used to identify
up-selling and cross-selling opportunities with existing customers
[Law01].
- Facilitating efficient browsing and searching of the web by
hierarchically clustering web-pages.
The challenges in both of these
applications mainly arise from two aspects:
- large numbers of data
samples,
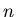 , and
, and
- each sample having a large number of
attributes or features (dimensions,
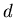 ).
).
Certain data mining
applications have the additional challenge of how to deal with
seasonality and other temporal variations in the data. This aspect is
not within the scope of this dissertation, but see [GG01].
The first aspect is typically dealt with by subsampling the data,
exploiting summary statistics, aggregating or `rolling up' to
consider data at a coarser resolution, or by using approximating
heuristics that reduce computation time at the cost of some loss in
quality. See [HKT01], chapter 8 for several examples of such
approaches.
The second aspect is typically addressed by reducing the number of
features, by either selection of a subset based on a suitable
criteria, or by transforming the original set of attributes into a
smaller one using linear projections (e.g., Principal Component
Analysis (PCA)) or through non-linear [CG01] means. Extensive
approaches for feature selection or extraction have been long studied,
particularly in the pattern recognition community
[YC74,MJ95,DHS01]. If these techniques succeed in
reducing the number of (derived) features to 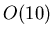 or less without
much loss of information, then a variety of clustering and
visualization methods can be applied to this reduced dimensionality
feature space. Otherwise, the problem may still be tractable if the
data is faithful to certain simplifying assumptions, most notably,
that either (i) the features are class- or cluster-conditionally
independent, or that (ii) most of the data can be accounted for by a
2- or 3-dimensional manifold within the high-dimensional embedding
space. The simplest example of case (i) is where the data is well
characterized by the superposition of a small number of Gaussian
components with identical and isotropic covariances, in which
case
or less without
much loss of information, then a variety of clustering and
visualization methods can be applied to this reduced dimensionality
feature space. Otherwise, the problem may still be tractable if the
data is faithful to certain simplifying assumptions, most notably,
that either (i) the features are class- or cluster-conditionally
independent, or that (ii) most of the data can be accounted for by a
2- or 3-dimensional manifold within the high-dimensional embedding
space. The simplest example of case (i) is where the data is well
characterized by the superposition of a small number of Gaussian
components with identical and isotropic covariances, in which
case  -means can be directly applied to a high-dimensional feature
space with good results. If the components have different covariance
matrices that are still diagonal (or else the number of parameters
will grow quadratically), unsupervised Bayes or mixture-density
modeling with EM, can be fruitfully applied. For situation (ii),
nonlinear PCA, Self-Organizing Map (SOM), Multi-Dimensional Scaling
(MDS) or more efficient custom formulations such as FASTMAP
[FL95], can be effectively applied.
This chapter primarily addresses the second aspect by describing an
alternate way of clustering and visualization when, even after
feature reduction, one is left with hundreds of dimensions per object
(and further reduction will significantly degrade the results), and
moreover, simplifying data modeling assumptions are also not valid. In
such situations, one is truly faced with the `curse of
dimensionality' issue [Fri94]. We have repeatedly encountered
such situations when examining retail industry market-basket data for
behavioral customer clustering, and also certain web-based data
collections.
Since clustering basically involves grouping objects based on their
inter-relationships or similarities, one can alternatively work in
similarity space instead of the original feature space. The key
insight in this work is that if one can find a similarity measure
(derived from the object features) that is appropriate for the problem
domain, then a single number can capture the essential `closeness'
of a given pair of objects, and any further analysis can be based only
on these numbers. The similarity space also lends itself to a simple
technique to visualize the clustering results. A major contribution
of this chapter is to demonstrate that this technique has increased
power when the clustering method used contains ordering information
(e.g., top-down). Popular clustering methods in feature space
are either non-hierarchical (as in
-means can be directly applied to a high-dimensional feature
space with good results. If the components have different covariance
matrices that are still diagonal (or else the number of parameters
will grow quadratically), unsupervised Bayes or mixture-density
modeling with EM, can be fruitfully applied. For situation (ii),
nonlinear PCA, Self-Organizing Map (SOM), Multi-Dimensional Scaling
(MDS) or more efficient custom formulations such as FASTMAP
[FL95], can be effectively applied.
This chapter primarily addresses the second aspect by describing an
alternate way of clustering and visualization when, even after
feature reduction, one is left with hundreds of dimensions per object
(and further reduction will significantly degrade the results), and
moreover, simplifying data modeling assumptions are also not valid. In
such situations, one is truly faced with the `curse of
dimensionality' issue [Fri94]. We have repeatedly encountered
such situations when examining retail industry market-basket data for
behavioral customer clustering, and also certain web-based data
collections.
Since clustering basically involves grouping objects based on their
inter-relationships or similarities, one can alternatively work in
similarity space instead of the original feature space. The key
insight in this work is that if one can find a similarity measure
(derived from the object features) that is appropriate for the problem
domain, then a single number can capture the essential `closeness'
of a given pair of objects, and any further analysis can be based only
on these numbers. The similarity space also lends itself to a simple
technique to visualize the clustering results. A major contribution
of this chapter is to demonstrate that this technique has increased
power when the clustering method used contains ordering information
(e.g., top-down). Popular clustering methods in feature space
are either non-hierarchical (as in  -means), or bottom-up
(agglomerative clustering). However, if one transforms the clustering
problem into a related problem of partitioning a similarity graph,
several powerful partitioning methods with ordering properties (as
described in the introductory paragraph) can be applied. Moreover,
the overall framework is quite generally applicable if one can
determine the appropriate similarity measure for a given
situation. This chapter applies it to three different domains (i)
clustering market-baskets (ii) web-documents and (iii) web-logs. In
each situation, a suitable similarity measure emerges from the
domain's specific needs.
The overall technique for clustering and visualization is linear
in the number of dimensions, but with respect to the number of data points,
-means), or bottom-up
(agglomerative clustering). However, if one transforms the clustering
problem into a related problem of partitioning a similarity graph,
several powerful partitioning methods with ordering properties (as
described in the introductory paragraph) can be applied. Moreover,
the overall framework is quite generally applicable if one can
determine the appropriate similarity measure for a given
situation. This chapter applies it to three different domains (i)
clustering market-baskets (ii) web-documents and (iii) web-logs. In
each situation, a suitable similarity measure emerges from the
domain's specific needs.
The overall technique for clustering and visualization is linear
in the number of dimensions, but with respect to the number of data points,
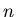 , it is quadratic in computational
and storage complexity.
This can become problematic for very large databases. Several
methods for reducing this complexity are outlined in section
3.6, but not elaborated upon much as that is not the
primary focus of this present work.
To make concrete some of the remarks above and motivate the rest of the
chapter, let us take a closer look at transactional data. A large
market-basket database may involve thousands of customers and
product-lines. Each record corresponds to a store visit by a customer,
so that customer could have multiple entries over time. The
transactional database can be conceptually viewed as a sparse
representation of a product (feature) by customer (object) matrix.
The
, it is quadratic in computational
and storage complexity.
This can become problematic for very large databases. Several
methods for reducing this complexity are outlined in section
3.6, but not elaborated upon much as that is not the
primary focus of this present work.
To make concrete some of the remarks above and motivate the rest of the
chapter, let us take a closer look at transactional data. A large
market-basket database may involve thousands of customers and
product-lines. Each record corresponds to a store visit by a customer,
so that customer could have multiple entries over time. The
transactional database can be conceptually viewed as a sparse
representation of a product (feature) by customer (object) matrix.
The 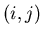 -th entry is non-zero only if customer
-th entry is non-zero only if customer 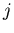 bought product
bought product
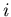 in that transaction. In that case, the entry represents pertinent
information such as quantity bought or extended price (quantity
in that transaction. In that case, the entry represents pertinent
information such as quantity bought or extended price (quantity
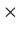 price) paid.
Since most customers only buy a small subset of these products during
any given visit, the corresponding feature vector (column) describing
such a transaction is (i) High-dimensional (large number of products),
but (ii) Sparse (most features are zero). (iii) Also, transactional
data typically has significant outliers, such as a few, big corporate
customers that appear in an otherwise small retail customer data.
Filtering these outliers may not be easy, nor desirable since they
could be very important (e.g., major revenue contributors). (iv) In
addition, features are often neither nominal nor continuous, but have
discrete positive ordinal attribute values, with a strongly
non-Gaussian distribution.
One way to reduce the feature space is to consider only the most
dominant products (attribute selection), but in practice this may
still leave hundreds of products to be considered. And since product
popularity tends to follow a Zipf distribution [Zip29], the tail
is `heavy', meaning that revenue contribution from the less
popular products is significant for certain customers. Moreover, in
retail the higher profit margins are often associated with less
popular products. One can do a `roll-up' to reduce number of
products, but with a corresponding loss in resolution or granularity.
Feature extraction or transformation is typically not carried out as
derived features lose the semantics of the original ones as well as
the sparsity property.
The alternative to attribute reduction is to try `simplification
via modeling'. One approach would be to only consider binary
features (bought or not). This reduces each transaction to an
unordered set of the purchased products. Thus one can use techniques
such as the a-priori algorithm to determine associations or rules. In
fact, this is currently the most popular approach to market-basket
analysis (see [BL97], chapter 8). Unfortunately, this results
in loss of vital information: one cannot differentiate between buying
1 gallon of milk and 100 gallons of milk, or one cannot weight
importance between buying an apple vs. buying a car, although clearly
these are very different situations from a business perspective. In
general, association-based rules derived from such sets will be
inferior when revenue or profits are the primary performance
indicators, since the simplified data representation loses information
about quantity, price or margins. The other broad class of modeling
simplifications for market-basket analysis is based on taking a
macro-level view of the data having characteristics capturable in a
small number of parameters. In retail, a 5-dimensional model for
customers composed from indicators for Recency, Frequency, Monetary
value, Variety, and Tenure (RFMVT) is popular. However, this useful
model is at a much lower resolution that looking at individual
products and fails to capture actual purchasing behavior in more
complex ways such as taste / brand preferences, or price sensitivity,
Due to all the above issues, traditional vector-space-based clustering
techniques work poorly on real-life market-basket data. For example,
a typical result of hierarchical agglomerative clustering (both
single-link and complete link approaches) on market-basket data is to
obtain one huge cluster near the origin, since most customers buy very
few items3.2, and a few scattered clusters otherwise. Applying
price) paid.
Since most customers only buy a small subset of these products during
any given visit, the corresponding feature vector (column) describing
such a transaction is (i) High-dimensional (large number of products),
but (ii) Sparse (most features are zero). (iii) Also, transactional
data typically has significant outliers, such as a few, big corporate
customers that appear in an otherwise small retail customer data.
Filtering these outliers may not be easy, nor desirable since they
could be very important (e.g., major revenue contributors). (iv) In
addition, features are often neither nominal nor continuous, but have
discrete positive ordinal attribute values, with a strongly
non-Gaussian distribution.
One way to reduce the feature space is to consider only the most
dominant products (attribute selection), but in practice this may
still leave hundreds of products to be considered. And since product
popularity tends to follow a Zipf distribution [Zip29], the tail
is `heavy', meaning that revenue contribution from the less
popular products is significant for certain customers. Moreover, in
retail the higher profit margins are often associated with less
popular products. One can do a `roll-up' to reduce number of
products, but with a corresponding loss in resolution or granularity.
Feature extraction or transformation is typically not carried out as
derived features lose the semantics of the original ones as well as
the sparsity property.
The alternative to attribute reduction is to try `simplification
via modeling'. One approach would be to only consider binary
features (bought or not). This reduces each transaction to an
unordered set of the purchased products. Thus one can use techniques
such as the a-priori algorithm to determine associations or rules. In
fact, this is currently the most popular approach to market-basket
analysis (see [BL97], chapter 8). Unfortunately, this results
in loss of vital information: one cannot differentiate between buying
1 gallon of milk and 100 gallons of milk, or one cannot weight
importance between buying an apple vs. buying a car, although clearly
these are very different situations from a business perspective. In
general, association-based rules derived from such sets will be
inferior when revenue or profits are the primary performance
indicators, since the simplified data representation loses information
about quantity, price or margins. The other broad class of modeling
simplifications for market-basket analysis is based on taking a
macro-level view of the data having characteristics capturable in a
small number of parameters. In retail, a 5-dimensional model for
customers composed from indicators for Recency, Frequency, Monetary
value, Variety, and Tenure (RFMVT) is popular. However, this useful
model is at a much lower resolution that looking at individual
products and fails to capture actual purchasing behavior in more
complex ways such as taste / brand preferences, or price sensitivity,
Due to all the above issues, traditional vector-space-based clustering
techniques work poorly on real-life market-basket data. For example,
a typical result of hierarchical agglomerative clustering (both
single-link and complete link approaches) on market-basket data is to
obtain one huge cluster near the origin, since most customers buy very
few items3.2, and a few scattered clusters otherwise. Applying
 -means could forcibly split this huge cluster into segments
depending on the initialization, but not in a meaningful manner.
In contrast, the similarity-based methods for both clustering and
visualization proposed in this chapter yield far better results for such
transactional data. While the methods have certain properties
tailored to such data-sets, they can also be applied to other higher
dimensional data-sets with similar characteristics. This is illustrated
by results on clustering text documents, each characterized by a bag-of-words
and represented by a vector of (suitably normalized) term
occurrences, often 1000 or more in length. Our detailed comparative
study in chapter 4 will show that in this domain traditional
clustering techniques also have some difficulties, though not as much as for
market-basket data since simplifying assumptions regarding class or
cluster conditional independence of features are not violated as much,
and consequently both Naive Bayes [MN98] and a normalized
version of
-means could forcibly split this huge cluster into segments
depending on the initialization, but not in a meaningful manner.
In contrast, the similarity-based methods for both clustering and
visualization proposed in this chapter yield far better results for such
transactional data. While the methods have certain properties
tailored to such data-sets, they can also be applied to other higher
dimensional data-sets with similar characteristics. This is illustrated
by results on clustering text documents, each characterized by a bag-of-words
and represented by a vector of (suitably normalized) term
occurrences, often 1000 or more in length. Our detailed comparative
study in chapter 4 will show that in this domain traditional
clustering techniques also have some difficulties, though not as much as for
market-basket data since simplifying assumptions regarding class or
cluster conditional independence of features are not violated as much,
and consequently both Naive Bayes [MN98] and a normalized
version of  -means [DM01] also show decent results. We
also apply the technique to clustering visitors to a website based on
their footprints, where, once a domain specific suitable similarity
metric is determined, the general technique again provides nice
results.
We begin by considering domain-specific transformations into
similarity space in section 3.2. Section
3.3 describes a specific clustering technique
(OPOSSUM), based on a multi-level graph partitioning algorithm
[KK98a]. In section 3.4, we describe a simple but
effective visualization technique that is applicable to similarity
spaces (CLUSION). Clustering and visualization results are
presented in section 3.5. In section 3.6,
we consider system issues and briefly discuss several strategies to
scale OPOSSUM for large data-sets.
-means [DM01] also show decent results. We
also apply the technique to clustering visitors to a website based on
their footprints, where, once a domain specific suitable similarity
metric is determined, the general technique again provides nice
results.
We begin by considering domain-specific transformations into
similarity space in section 3.2. Section
3.3 describes a specific clustering technique
(OPOSSUM), based on a multi-level graph partitioning algorithm
[KK98a]. In section 3.4, we describe a simple but
effective visualization technique that is applicable to similarity
spaces (CLUSION). Clustering and visualization results are
presented in section 3.5. In section 3.6,
we consider system issues and briefly discuss several strategies to
scale OPOSSUM for large data-sets.




Next: Domain Specific Features and
Up: Relationship-based Clustering and Visualization
Previous: Relationship-based Clustering and Visualization
Contents
Alexander Strehl
2002-05-03