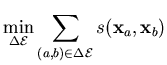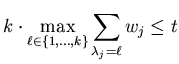Next: Determining the Number of
Up: OPOSSUM
Previous: Balancing
Contents
Vertex Weighted Graph Partitioning
We map the problem of clustering to partitioning a vertex weighted
graph
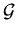 into
into  unconnected components of approximately
equal size (as defined by the balancing constraint) by removing a
minimal amount of edges. The objects to be clustered are viewed as
a set of vertices
unconnected components of approximately
equal size (as defined by the balancing constraint) by removing a
minimal amount of edges. The objects to be clustered are viewed as
a set of vertices
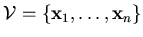 . Two vertices
. Two vertices
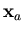 and
and
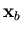 are connected with an undirected edge
are connected with an undirected edge
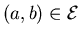 of positive weight given by the similarity
of positive weight given by the similarity
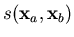 . This defines the graph
. This defines the graph
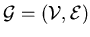 . An edge separator
. An edge separator
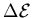 is
a set of edges whose removal splits the graph
is
a set of edges whose removal splits the graph
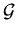 into
into  pair-wise unconnected components (sub-graphs)
pair-wise unconnected components (sub-graphs)
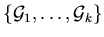 . All sub-graphs
. All sub-graphs
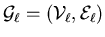 have
pairwise disjoint sets of vertices and edges. The edge separator for a
particular partitioning includes all the edges that are not part of
any sub-graph, or
have
pairwise disjoint sets of vertices and edges. The edge separator for a
particular partitioning includes all the edges that are not part of
any sub-graph, or
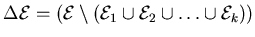 .
The clustering task is thus to find an edge separator with a minimum
sum of edge weights, that partitions the graph into
.
The clustering task is thus to find an edge separator with a minimum
sum of edge weights, that partitions the graph into  disjoint
pieces. The following equation formalizes this minimum cut objective:
disjoint
pieces. The following equation formalizes this minimum cut objective:
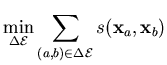 |
(3.3) |
Without loss of generality, we can assume that the vertex weights
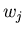 are normalized to sum up to
are normalized to sum up to 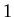 :
:
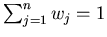 . While
striving for the minimum cut objective, the balancing constraint
. While
striving for the minimum cut objective, the balancing constraint
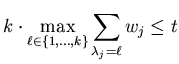 |
(3.4) |
has to be fulfilled. The left hand side of the inequality is called
the imbalance (the ratio of the biggest cluster in terms of cumulative
normalized edge weight to the desired equal cluster-size 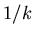 ) and
has a lower bound of 1. The balancing threshold
) and
has a lower bound of 1. The balancing threshold 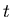 enforces perfectly
balanced clusters for
enforces perfectly
balanced clusters for 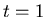 . In practice
. In practice 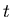 is often chosen to be
slightly greater than 1 (e.g., we use
is often chosen to be
slightly greater than 1 (e.g., we use 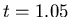 for all our experiments
which allows at most 5% of imbalance).
Thus, in graph partitioning one has to essentially solve a constrained
optimization problem. Finding such an optimal partitioning is an
NP-hard problem [GJ79]. However, there are fast, heuristic
algorithms for this widely studied problem.
We experimented with the Kernighan-Lin (KL) algorithm, recursive
spectral bisection, and multi-level
for all our experiments
which allows at most 5% of imbalance).
Thus, in graph partitioning one has to essentially solve a constrained
optimization problem. Finding such an optimal partitioning is an
NP-hard problem [GJ79]. However, there are fast, heuristic
algorithms for this widely studied problem.
We experimented with the Kernighan-Lin (KL) algorithm, recursive
spectral bisection, and multi-level  -way partitioning (METIS).
The basic idea in KL [KL70] to dealing with graph
partitioning is to construct an initial partition of the vertices
either randomly or according to some problem-specific strategy. Then
the algorithm sweeps through the vertices, deciding whether the size
of the cut would increase or decrease if we moved this vertex
-way partitioning (METIS).
The basic idea in KL [KL70] to dealing with graph
partitioning is to construct an initial partition of the vertices
either randomly or according to some problem-specific strategy. Then
the algorithm sweeps through the vertices, deciding whether the size
of the cut would increase or decrease if we moved this vertex
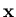 over to another partition. The decision to move
over to another partition. The decision to move
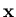 can be made in time proportional to its degree by simply
counting whether more of
can be made in time proportional to its degree by simply
counting whether more of
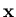 's neighbors are on the same
partition as
's neighbors are on the same
partition as
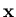 or not. Of course, the desirable side for
or not. Of course, the desirable side for
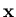 will change if many of its neighbors switch, so multiple
passes are likely to be needed before the process converges to a local
optimum.
In recursive bisection, a
will change if many of its neighbors switch, so multiple
passes are likely to be needed before the process converges to a local
optimum.
In recursive bisection, a  -way split is obtained by recursively
partitioning the graph into two subgraphs. Spectral bisection
[PSL90,HL95] uses the eigenvector associated with the
second smallest eigenvalue of the graph's Laplacian (Fiedler vector)
[Fie75] for splitting.
METIS [KK98a] handles multi-constraint
multi-objective graph partitioning in three phases: (i) coarsening,
(ii) initial partitioning, and (iii) refining. First a sequence of
successively smaller and therefore coarser graphs is constructed
through heavy-edge matching. Secondly, the initial partitioning is
constructed using one out of four heuristic algorithms (three based on
graph growing and one based on spectral bisection). In the third phase
the coarsened partitioned graph undergoes boundary Kernighan-Lin
refinement. In this last phase vertices are only swapped amongst
neighboring partitions (boundaries). This ensures that neighboring
clusters are more related than non-neighboring clusters. This ordering
property is beneficial for visualization, as explained in subsection
3.6.1. In contrast, since recursive bisection computes a
bisection of a subgraph at a time, its view is limited. Thus, it can
not fully optimize the partition ordering and the global constraints.
This renders it less effective for our purposes. Also, we found the
multi-level partitioning to deliver the best partitionings as well as
to be the fastest and most scalable of the three choices we
investigated. Hence, METIS is used as the graph partitioner in
OPOSSUM.
-way split is obtained by recursively
partitioning the graph into two subgraphs. Spectral bisection
[PSL90,HL95] uses the eigenvector associated with the
second smallest eigenvalue of the graph's Laplacian (Fiedler vector)
[Fie75] for splitting.
METIS [KK98a] handles multi-constraint
multi-objective graph partitioning in three phases: (i) coarsening,
(ii) initial partitioning, and (iii) refining. First a sequence of
successively smaller and therefore coarser graphs is constructed
through heavy-edge matching. Secondly, the initial partitioning is
constructed using one out of four heuristic algorithms (three based on
graph growing and one based on spectral bisection). In the third phase
the coarsened partitioned graph undergoes boundary Kernighan-Lin
refinement. In this last phase vertices are only swapped amongst
neighboring partitions (boundaries). This ensures that neighboring
clusters are more related than non-neighboring clusters. This ordering
property is beneficial for visualization, as explained in subsection
3.6.1. In contrast, since recursive bisection computes a
bisection of a subgraph at a time, its view is limited. Thus, it can
not fully optimize the partition ordering and the global constraints.
This renders it less effective for our purposes. Also, we found the
multi-level partitioning to deliver the best partitionings as well as
to be the fastest and most scalable of the three choices we
investigated. Hence, METIS is used as the graph partitioner in
OPOSSUM.




Next: Determining the Number of
Up: OPOSSUM
Previous: Balancing
Contents
Alexander Strehl
2002-05-03