



Next: Similarity Measures for Document
Up: Impact of Similarity Measures
Previous: Impact of Similarity Measures
Contents
Motivation
Document clusters can provide a structure for organizing large bodies
of text for efficient browsing and searching. For example, recent
advances in Internet search engines (e.g., http://vivisimo.com/, http://metacrawler.com/) exploit document cluster analysis.
For this purpose, a document is commonly represented as a vector
consisting of the suitably normalized frequency counts of words or
terms. Each document typically contains only a small percentage of
all the words ever used. If we consider each document as a
multi-dimensional vector and then try to cluster documents based on
their word contents, the problem differs from classic clustering
scenarios in several ways: Document data is
high-dimensional4.2,
characterized by a very sparse
term-document matrix with positive ordinal attribute values and a
significant amount of outliers.
In such situations, one is truly faced with the `curse of
dimensionality' issue [Fri94] since, even after feature
reduction, one is left with hundreds of dimensions per object.
In the previous chapter, we developed the relationship-clustering
framework to effectively side-step the `curse of dimensionality'. In
the relationship-based clustering process, key cluster analysis activities
[JD88] can be associated with each step:
- To obtain features
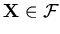 from the raw objects, a suitable object representation has to be found. We will not be concerned with
representation in this chapter, since the significant amount of
empirical studies on document clustering in the 80s and earlier
emphasized various ways of representing / normalizing documents
[Wil88,SB88,Sal89].
from the raw objects, a suitable object representation has to be found. We will not be concerned with
representation in this chapter, since the significant amount of
empirical studies on document clustering in the 80s and earlier
emphasized various ways of representing / normalizing documents
[Wil88,SB88,Sal89].
- In the second step, a measure of proximity
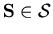 has to be defined between objects.
The choice of similarity or distance can have a profound impact on
clustering quality. In this chapter, we first compare
similarity measures analytically and then illustrate their semantics
geometrically.
has to be defined between objects.
The choice of similarity or distance can have a profound impact on
clustering quality. In this chapter, we first compare
similarity measures analytically and then illustrate their semantics
geometrically.
- The third activity requires a suitable
choice of clustering algorithm to obtain cluster labels
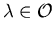 .
Agglomerative clustering approaches were historically
dominant as they compared favorably with flat partitional approaches on
small or medium sized collections [Wil88,Ras92]. But lately,
some new partitional methods have emerged (spherical
.
Agglomerative clustering approaches were historically
dominant as they compared favorably with flat partitional approaches on
small or medium sized collections [Wil88,Ras92]. But lately,
some new partitional methods have emerged (spherical  -means, graph
partitioning-based, etc.) that have attractive properties in terms of
both quality and scalability and can work with a wider range of
similarity measures. In addition, much larger document collections
are being generated.4.3
This warrants
an updated comparative study on text clustering, which is the
motivation behind this chapter.
-means, graph
partitioning-based, etc.) that have attractive properties in terms of
both quality and scalability and can work with a wider range of
similarity measures. In addition, much larger document collections
are being generated.4.3
This warrants
an updated comparative study on text clustering, which is the
motivation behind this chapter.
- Finally, in the assessment of output one has to investigate the
validity of the results.4.4In this chapter, we propose an
experimental methodology to compare high-dimensional clusterings based
on mutual information and we show how this is better than purity or
entropy-based measures [BGG$^+$99,ZK01,SKK00]. Finally,
we conduct a series of experiments to evaluate the performance and
cluster quality of four similarity measures (Euclidean, cosine,
Pearson correlation, extended Jaccard) in combination with five
algorithms (random, self-organizing map, hypergraph partitioning,
generalized
 -means, weighted graph partitioning).
-means, weighted graph partitioning).
Some very recent, notable comparative studies on document clustering
[SKK00,ZK01] also consider some of the newer issues. Our
work is distinguished from these efforts mainly by its focus on the
key role of the similarity measures involved, emphasis on balancing,
and the use of a normalized mutual information-based evaluation that
we believe has superior properties.
The basic notation is the same as introduced in the previous chapter
in section 3.2.
In the next section, we introduce several similarity measures,
illustrate some of their properties, and show why we are interested in
some but not others. In section 4.3, the algorithms
using these similarity measures are discussed. Section
4.4 introduces a variety of cluster quality evaluation methods
including our proposed mutual information criterion. Finally, the
experiments and results are shown in section
4.5.




Next: Similarity Measures for Document
Up: Impact of Similarity Measures
Previous: Impact of Similarity Measures
Contents
Alexander Strehl
2002-05-03