Results

In this section, we present and compare the results of the eleven approaches on the four document data-sets. Clustering quality is understood in terms of mutual information and balance. For each data-set we set the number of clusters $k$ to be twice the number of categories $g$, except for the REUT data-set where we used $k=40$ since there are many small categories. Using a greater number of clusters than classes allows multi-modal distributions for each class. For example, in an XOR like problem, there are two classes, but four clusters.

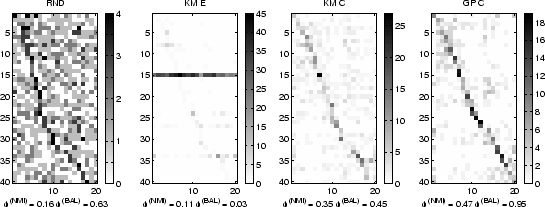
Let us first look at a representative result to illustrate the behavior of some algorithms and our evaluation methodology. In figure 4.3, confusion matrices illustrating quality differences of RND, KM E, KM C, and GP C approaches on a sample of 800 documents from N20 are shown. The horizontal and vertical axis correspond to the categories and clusters, respectively. Clusters are sorted in increasing order of dominant category. Entries indicate the number $n_{\ell}^{(h)}$ of documents in cluster $\ell$ and category $h$ by darkness. Expectedly, random partitioning RND results in indiscriminating clusters with a mutual information score $\phi^{(\mathrm{NMI})} = 0.16$. The purity score $\phi^{(\mathrm{A})} = 0.16$ indicates that on average the dominant category contributes 16% of the objects in a cluster. However, since labels are drawn from a uniform distribution, cluster sizes are somewhat balanced with $\phi^{(\mathrm{BAL})} = 0.63$. KM E delivers one large cluster (cluster 15) and many small clusters with $\phi^{(\mathrm{BAL})} = 0.03$. This strongly imbalanced clustering is characteristic for KM E on high-dimensional sparse data and is problematic because it usually defeats certain application specific purposes such as browsing. It also results in sub-random quality $\phi^{(\mathrm{NMI})} = 0.11$ ( $\phi^{(\mathrm{A})} = 0.17$). KM C results are good. A `diagonal' can be clearly seen in the confusion matrix. This indicates that the clusters align with the ground truth categorization which is reflected by an overall mutual information $\phi^{(\mathrm{NMI})} = 0.35$ ( $\phi^{(\mathrm{A})} = 0.38$). Balancing is good as well with $\phi^{(\mathrm{BAL})} = 0.45$. GP C exceeds KM C in both aspects with $\phi^{(\mathrm{NMI})} = 0.47$ ( $\phi^{(\mathrm{A})} = 0.48$) as well as balance $\phi^{(\mathrm{BAL})} = 0.95$. The `diagonal' is stronger and clusters are very balanced.

Figure 4.3: Confusion matrices illustrating quality differences of RND, KM E, KM C, and GP C approaches on a sample of 800 documents from N20. Matrix entries indicate the number $n_{\ell}^{(h)}$ of documents in cluster $\ell$ (row) and category $h$ (column) by darkness. Clusters are sorted in ascending order of their dominant category. KM E delivers one large cluster and shows sub-random quality $\phi^{(\mathrm{NMI})}$. KM C results are good, but are exceeded by GP C in terms of mutual information $\phi^{(\mathrm{NMI})}$ as well as balance $\phi^{(\mathrm{BAL})}$.

The rest of the results are given in summarized form instead of the more detailed treatment in the example above, since the comparative trends are very clear even at this macro level. Some examples of detailed confusion matrices and pairwise t-tests can be found in our earlier work [SGM00].

For a systematic comparison, ten experiments were performed for each of the random samples of sizes 50, 100, 200, 400, and 800. Figure 4.4 shows performance curves in terms of (relative) mutual information comparing 10 algorithms on 4 data sets. Each curve shows the difference $\Delta \phi^{(\mathrm{NMI})}$ in mutual information-based quality $\phi^{(\mathrm{NMI})}$ compared to random partitioning for 5 sample sizes (at 50, 100, 200, 400, and 800). Error bars indicate $\pm$1 standard deviations over 10 experiments. Figure 4.5 shows quality in terms of balance for 4 data sets in combination with 10 algorithms. Each curve shows the cluster balance $\phi^{(\mathrm{BAL})}$ for 5 sample sizes (again at 50, 100, 200, 400, and 800). Error bars indicate $\pm$1 standard deviations over 10 experiments. Figure 4.6 summarizes the results on all four data-sets at the highest sample size level ($n=800$). We also conducted pairwise t-tests at $n=800$ to assure differences in average performance are significant. For illustration and brevity, we chose to show mean performance with standard variation bars rather than the t-test results (see our previous work [SGM00]).

First, we look at quality in terms of mutual information (figures 4.4, 4.6(a)). With increasing sample size $n$, the quality of clusterings tends to improve. Non-metric (cosine, correlation, Jaccard) graph partitioning approaches work best on text data ( $n=800:\Delta \phi^{(\mathrm{NMI})} \approx 0.3$) followed by non-metric $k$-means approaches. Clearly, a non-metric e.g., dot-product-based similarity measure is necessary for good quality. Due to the conservative normalization, depending on the given data-set the maximum obtainable mutual information (for a perfect classifier!) tends to be around 0.8 to 0.9. A mutual information-based quality around 0.4 and 0.5 (which is approximately 0.3 to 0.4 better than random at $n=800$) is an excellent result.^4.7Hypergraph partitioning constitutes the third tier. Euclidean techniques including SOM perform rather poorly. Surprisingly, the SOM still delivers significantly better than random results despite the limited expressiveness of the implicitly used Euclidean distances. The success of SOM is explained with the fact that the Euclidean distance becomes locally meaningful once the cell-centroids are locked onto a good cluster.

All approaches behaved consistently over the four data-sets with only slightly different scale caused by the different data-sets' complexities. The performance was best on YAHOO and WEBKB followed by N20 and REUT. Interestingly, the gap between GP and KM techniques is wider on YAHOO than on WEBKB. The low performance on REUT is probably due to the high number of classes (82) and their widely varying sizes.

In order to assess which approaches are more suitable for a particular amount of objects $n$, we also looked for intersects in the performance curves of the top algorithms (non-metric GP and KM, HGP).^4.8In our experiments, the curves do not intersect indicating that ranking of the top performers does not change in the range of data-set sizes considered.

In terms of balance (figures 4.5, 4.6(b)) the advantages of graph partitioning are clear. Graph partitioning explicitly tries to achieve balanced clusters ( $n=800:\phi^{(\mathrm{BAL})} \approx 0.9$). The second tier is hypergraph partitioning which is also a balanced technique ( $n=800:\phi^{(\mathrm{BAL})} \approx 0.7$) followed by non-metric $k$-means approaches ( $n=800:\phi^{(\mathrm{BAL})} \approx 0.5$). Poor balancing is shown by SOM and Euclidean $k$-means ( $n=800:\phi^{(\mathrm{BAL})} \approx 0.1$). Interestingly, balancedness does not change significantly for the $k$-means-based approaches as the number of samples $n$ increases. Graph partitioning based approaches quickly approach perfect balancing as would be expected since they are explicitly designed to do so.

Non-metric graph partitioning is significantly better in terms of mutual information as well as in balance. There is no significant difference in performance amongst the non-metric similarity measures using cosine, correlation, and extended Jaccard. Euclidean distance based approaches do not perform better than random clustering.

Figure 4.4: Mutual information performance curves comparing 10 algorithms on 4 data-sets. Each curve shows the difference in mutual information-based quality $\phi^{(\mathrm{NMI})}$ compared to random for 5 sample sizes (at 50, 100, 200, 400, and 800). Error bars indicate $\pm$1 standard deviations over 10 experiments.

N20
WEBKB
YAHOO
REUT

Figure 4.5: Amount of balancing achieved for 4 data-sets in combination with 10 algorithms. Each curve shows the cluster balance $\phi^{(\mathrm{BAL})}$ for 5 sample sizes (at 50, 100, 200, 400, and 800). Error bars indicate $\pm$1 standard deviations over 10 experiments.

N20
WEBKB
YAHOO
REUT

Figure 4.6: Comparison of cluster quality in terms of (a) mutual information and (b) balance on average over 4 data-sets with 10 trials each at 800 samples. Error-bars indicate $\pm$1 standard deviation. Graph partitioning is significantly better in terms of mutual information as well as in balance. Euclidean distance based approaches do not perform better than random clustering.

(a)	(b)