The notion of integrating multiple data sources and/or learned models is found in several disciplines, for example, the combining of estimators in econometrics [Gra89], evidences in rule-based systems [Bar81] and multi-sensor data fusion [Das94]. A simple but effective type of such multi-learner systems are ensembles, wherein each component learner (typically a regressor or classifier) tries to solve the same task. Each learner may receive somewhat different subsets of the data for `training' or parameter estimation (as in bagging [Bre94] and boosting [DCJ$^+$94]), and may use different feature extractors on the same raw data. The system output is determined by combining the outputs of the individual learners via a variety of methods including voting, (weighted) averaging, order statistics, product rule, entropy, and stacking. In the past few years, a host of experimental results have shown that such ensembles provide statistically significant improvements in performance along with tighter confidence intervals, especially when the component models are `unstable' [Wol92,GBC92,Sha96,CS95]. Moreover, theoretical analysis has been developed for both regression [Per93,Has93] and classification [TG96] to estimate the gains achievable. Combining is an effective way of reducing model variance, and in certain situations it also reduces bias [Per93,TG99]. It works best when each learner is well trained, but different learners generalize in different ways, i.e., there is diversity in the ensemble [KV95,Die01].
In unsupervised learning, the clustering problem is concerned with
partitioning a set of objects
![]() into
into ![]() disjoint5.2groups / clusters
disjoint5.2groups / clusters
![]() such
that similar objects are in the same cluster while dissimilar objects
are in different clusters.
Clustering is often posed as an optimization problem by defining a
suitable error criterion to be minimized. Using this formulation,
many standard algorithms such as
such
that similar objects are in the same cluster while dissimilar objects
are in different clusters.
Clustering is often posed as an optimization problem by defining a
suitable error criterion to be minimized. Using this formulation,
many standard algorithms such as ![]() -means and agglomerative
clustering have been established over the past forty years
[Eve74,JD88]. Recent interest in the data mining community
has lead to a new breed of approaches such as CLARANS, DBScan, BIRCH,
CLIQUE, and WaveCluster [RS99], that are oriented towards
clustering large data-sets kept in databases and emphasize
scalability.
-means and agglomerative
clustering have been established over the past forty years
[Eve74,JD88]. Recent interest in the data mining community
has lead to a new breed of approaches such as CLARANS, DBScan, BIRCH,
CLIQUE, and WaveCluster [RS99], that are oriented towards
clustering large data-sets kept in databases and emphasize
scalability.
Unlike classification problems, there are no well known approaches to combining multiple clusterings. We call the combination of multiple partitionings of the same underlying set of objects without accessing the original features as the cluster ensemble design problem. Since the combiner has no more access to the original features and only cluster labels are available, this is a framework for knowledge reuse [BG99]. This problem is more difficult than designing classifier ensembles since cluster labels are symbolic and so one must also solve a correspondence problem. In addition, the number and shape of clusters provided by the individual solutions may vary based on the clustering method as well as on the particular view of the data presented to that method. Moreover, the desired number of clusters is often not known in advance. In fact, the `right' number of clusters in a data-set depends on the scale at which the data is inspected, and sometimes, equally valid (but substantially different) answers can be obtained for the same data [CG96].
A clusterer consists of a particular clustering algorithm with a specific view of the data. A clustering is the output of a clusterer and consists of the group labels for some or all objects (a labeling). Cluster ensembles provide a tool for consolidation of results from a portfolio of individual clustering results. It is useful in a variety of contexts:
It is well known that no clustering method is perfect, and the
performance of a given method can vary significantly across data-sets. For example, the popular ![]() -means algorithm that performs
respectably in several applications, has an underlying assumption that
the data (after appropriate normalization such as using Mahalanobis
distance) is generated by a mixture of
-means algorithm that performs
respectably in several applications, has an underlying assumption that
the data (after appropriate normalization such as using Mahalanobis
distance) is generated by a mixture of ![]() Gaussians, each having
identical, isotropic covariance matrices. If the actual data
distribution is very different from this generative model, then, even
with the `correct' guess for
Gaussians, each having
identical, isotropic covariance matrices. If the actual data
distribution is very different from this generative model, then, even
with the `correct' guess for ![]() , its performance can be worse than
a random partitioning, specially in sparse, high dimensional
spaces (see chapter 3). In fact, for difficult data-sets,
comparative studies across multiple clustering algorithms typically
show much more variability in results than comparative studies on
multiple classification methods, where any good approximator of
Bayesian a posteriori class probabilities will provide comparable
results [RL91]. Thus there should be a potential for greater
gains when using an ensemble for clustering problems.
, its performance can be worse than
a random partitioning, specially in sparse, high dimensional
spaces (see chapter 3). In fact, for difficult data-sets,
comparative studies across multiple clustering algorithms typically
show much more variability in results than comparative studies on
multiple classification methods, where any good approximator of
Bayesian a posteriori class probabilities will provide comparable
results [RL91]. Thus there should be a potential for greater
gains when using an ensemble for clustering problems.
A different but related motivation for using a cluster ensemble is to build a robust
clustering portfolio that can perform well over a wide range of data-sets with little hand-tuning.
For example, by using an ensemble that includes approaches
suitable for low-dimensional, metric spaces (e.g., ![]() -means, SOM
[Koh95], DBSCAN [EKSX96]) as well as algorithms tailored for
high-dimensional, sparse spaces (e.g., spherical
-means, SOM
[Koh95], DBSCAN [EKSX96]) as well as algorithms tailored for
high-dimensional, sparse spaces (e.g., spherical ![]() -means
[DM01], and Jaccard-based graph partitioning (e.g., see chapter 3), one may
perform very well in 3D as well as in 30000D spaces without having to switch models.
This characteristic is very attractive in practical settings.
-means
[DM01], and Jaccard-based graph partitioning (e.g., see chapter 3), one may
perform very well in 3D as well as in 30000D spaces without having to switch models.
This characteristic is very attractive in practical settings.
A cluster ensemble can combine individual results from the distributed computing entities, under two scenarios:
Contributions. The idea of integrating independently computed clusterings into a combined clustering leads us to a general knowledge reuse framework that we call the cluster ensemble. Our contribution in this chapter is to formally define the design of a cluster ensemble as an optimization problem and to propose three effective and efficient frameworks for solving it. We show how any set of clusterings can be represented as a hypergraph. Using this hypergraph, three methods are proposed for computing a combined clustering based on similarity-based reclustering, hypergraph partitioning, and meta-clustering, respectively. We also describe applications of cluster ensembles for each of the three application scenarios described above and show results on real data.
Notation.
Let
![]() denote a set of
objects / samples / points. A partitioning of these
denote a set of
objects / samples / points. A partitioning of these ![]() objects into
objects into ![]() clusters can be represented as a set of
clusters can be represented as a set of ![]() sets of objects
sets of objects
![]() or as a label vector
or as a label vector
![]() . We also refer to a
clustering / labeling as a model. A clusterer
. We also refer to a
clustering / labeling as a model. A clusterer ![]() is a function that
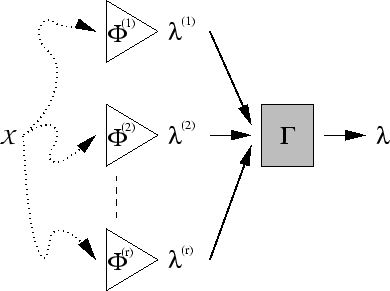
delivers a label vector given an ordered set of objects. Figure
5.1 shows the basic setup of the cluster ensemble:
A set of
is a function that
delivers a label vector given an ordered set of objects. Figure
5.1 shows the basic setup of the cluster ensemble:
A set of ![]() labelings
labelings
![]() is combined
into a single labeling
is combined
into a single labeling
![]() using a consensus function
using a consensus function
![]() . We call the original set of labelings, the profile and
the resulting single labeling, the consensus
clustering. Vector / matrix transposition is indicated with a
superscript
. We call the original set of labelings, the profile and
the resulting single labeling, the consensus
clustering. Vector / matrix transposition is indicated with a
superscript ![]() . A superscript in brackets denotes an index and
not an exponent.
. A superscript in brackets denotes an index and
not an exponent.
|
Organization. In the next section, we will introduce the
cluster ensemble problem in more detail and in section
5.3 we propose and compare three possible combining schemes, ![]() .
In section 5.4 we will apply these schemes to both
centralized and distributed clustering problems and present case
studies on a variety of data-sets to highlight these applications.
.
In section 5.4 we will apply these schemes to both
centralized and distributed clustering problems and present case
studies on a variety of data-sets to highlight these applications.