



Next: Mixture Density Estimation
Up: Clustering Algorithms
Previous: Artificial Neural Systems
Contents
In many domains, the high-dimensional representation contains
redundant information considering the clustering task. In document
clustering, for example, many different words and phrases can be used
to convey a similar meaning. Hence, the vector-space representation
contains highly correlated evidence and the clustering process can be
extended as follows:
- Find an appropriate projection of the original data (
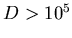 )
into concept space (
)
into concept space (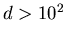 ).
).
- Perform clustering in the dimensionality reduced space.
Good sub-spaces for projections are characterized by preserving most
of the `information' in the data. For a regular matrix the  eigenvectors with the
eigenvectors with the  highest eigenvalues are the
highest eigenvalues are the 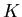 orthogonal
directions of projection that explain the maximum possible of the
variance in the data [Str88]. The extension of the eigen
decomposition to non-square matrices is the Singular Value
Decomposition (SVD). SVD is closely related to
Principal Component Analysis (PCA) which is based on the
SVD of the zero-mean normalized data. In Latent Semantic
Indexing (LSI) the
orthogonal
directions of projection that explain the maximum possible of the
variance in the data [Str88]. The extension of the eigen
decomposition to non-square matrices is the Singular Value
Decomposition (SVD). SVD is closely related to
Principal Component Analysis (PCA) which is based on the
SVD of the zero-mean normalized data. In Latent Semantic
Indexing (LSI) the
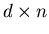 word-document matrix
word-document matrix
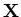 is modeled by a rank-
is modeled by a rank-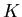 approximation using the top
approximation using the top 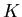 singular values. While LSI is originally used for improved
query processing in information retrieval the base idea may be
employed for clustering as well. A matrix
singular values. While LSI is originally used for improved
query processing in information retrieval the base idea may be
employed for clustering as well. A matrix
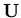 is unitary if
and only if
is unitary if
and only if
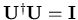 . Equation
2.4 gives the singular value decomposition (SVD)
of the
. Equation
2.4 gives the singular value decomposition (SVD)
of the
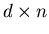 data matrix
data matrix
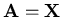 into a product
of the unitary
into a product
of the unitary
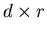 matrix
matrix
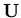 , the diagonal
, the diagonal
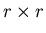 matrix
matrix
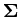 , and the unitary
, and the unitary
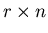 matrix
matrix
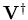 .
.
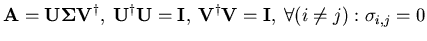 |
(2.4) |
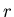 is the rank of
is the rank of
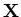 .
.
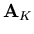 is the best rank
is the best rank
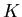 -approximation of
-approximation of
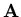 (with
(with 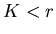 ) which is obtained by
using
) which is obtained by
using
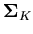 , which is
, which is
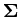 with the
original upper-left
with the
original upper-left 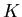 diagonal entries and all others set to 0
(equation 2.5)
diagonal entries and all others set to 0
(equation 2.5)
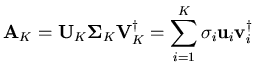 |
(2.5) |
The left-singular column vectors
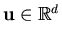 in
in
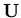 are called the concept vectors with
are called the concept vectors with
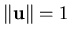 .
In general,
.
In general,
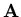 looses its sparsity since the projection is
not axis-parallel. However, the concept space does not have to be
instantiated explicitly, but can be rather stored functionally, as for
example, a product of two sparse matrices.
In the vector space model [SWY75,Kol97], a keyword search
can be expressed as a matrix product as shown in
2.6. A binary valued query vector
looses its sparsity since the projection is
not axis-parallel. However, the concept space does not have to be
instantiated explicitly, but can be rather stored functionally, as for
example, a product of two sparse matrices.
In the vector space model [SWY75,Kol97], a keyword search
can be expressed as a matrix product as shown in
2.6. A binary valued query vector
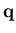 is
projected linearly to a match vector
is
projected linearly to a match vector
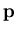 .
.
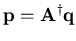 |
(2.6) |
In the context of web-search, it has been claimed that projecting the
query vector and the web-page vectors to concept space outperforms
keyword search. The rationale for this observation lies in the fact
that the rank-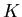 approximation is actually more representative than
the original data matrix, because noise and redundancy have been
removed. Also, it has been argued that by reducing the matrix
complexity to a small number of concepts, implicitly the query is
extended to encompass redundancy as introduced e.g., by synonyms.
Using the optimal rank-
approximation is actually more representative than
the original data matrix, because noise and redundancy have been
removed. Also, it has been argued that by reducing the matrix
complexity to a small number of concepts, implicitly the query is
extended to encompass redundancy as introduced e.g., by synonyms.
Using the optimal rank-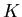 -approximation (LSI) yields
equation 2.7, where
-approximation (LSI) yields
equation 2.7, where
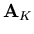 is given by equation
2.5.
is given by equation
2.5.
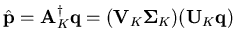 |
(2.7) |
Generally, the rank of 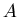 has a magnitude of
has a magnitude of 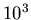 to
to 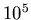 and
and 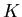 is around
is around 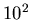 . Recently, it has been reported that random subspace
projections perform very well for high-dimensional data and are close
to the optimal projection as given by the SVD [SS97].
. Recently, it has been reported that random subspace
projections perform very well for high-dimensional data and are close
to the optimal projection as given by the SVD [SS97].




Next: Mixture Density Estimation
Up: Clustering Algorithms
Previous: Artificial Neural Systems
Contents
Alexander Strehl
2002-05-03
![]() has a magnitude of
has a magnitude of ![]() to
to ![]() and
and ![]() is around
is around ![]() . Recently, it has been reported that random subspace
projections perform very well for high-dimensional data and are close
to the optimal projection as given by the SVD [SS97].
. Recently, it has been reported that random subspace
projections perform very well for high-dimensional data and are close
to the optimal projection as given by the SVD [SS97].