Next: Comparison
Up: CLUSION: Cluster Visualization
Previous: Coarse Seriation
Contents
The seriation of the similarity matrix,
 , is very useful
for visualization. Since the similarity matrix is 2-dimensional, it
can be readily visualized as a gray-level image where a white (black)
pixel corresponds to minimal (maximal) similarity of 0 (1). The
darkness (gray level value) of the pixel at row
, is very useful
for visualization. Since the similarity matrix is 2-dimensional, it
can be readily visualized as a gray-level image where a white (black)
pixel corresponds to minimal (maximal) similarity of 0 (1). The
darkness (gray level value) of the pixel at row  and column
and column  increases with the similarity between the samples
increases with the similarity between the samples
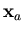 and
and
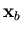 .
When looking at the image it is useful to consider the similarity
.
When looking at the image it is useful to consider the similarity 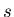 as a random variable taking values from 0 to 1. The expected
similarity within cluster
as a random variable taking values from 0 to 1. The expected
similarity within cluster 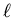 is thus represented by the
average intensity within a square region with side length
is thus represented by the
average intensity within a square region with side length 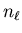 ,
around the main diagonal of the matrix. The off-diagonal rectangular
areas visualize the relationships between clusters. The
brightness distribution in the rectangular areas yields insight
towards the quality of the clustering and possible improvements. In
order to make these regions apparent, thin red horizontal and vertical
lines are used to show the divisions into the rectangular
regions3.3. Visualizing similarity space in this way can help
to quickly get a feel for the clusters in the data. Even for a large
number of points, a sense for the intrinsic number of clusters
,
around the main diagonal of the matrix. The off-diagonal rectangular
areas visualize the relationships between clusters. The
brightness distribution in the rectangular areas yields insight
towards the quality of the clustering and possible improvements. In
order to make these regions apparent, thin red horizontal and vertical
lines are used to show the divisions into the rectangular
regions3.3. Visualizing similarity space in this way can help
to quickly get a feel for the clusters in the data. Even for a large
number of points, a sense for the intrinsic number of clusters  in
a data-set can be gained.
in
a data-set can be gained.
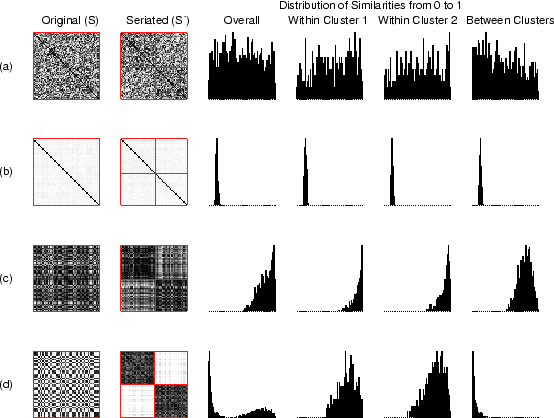
Figure 3.2:
Illustrative CLUSION patterns in original order and
seriated using optimal bipartitioning are shown in the left two
columns. The right four columns show corresponding similarity
distributions. In each example there are 50 objects: (a) no natural
clusters (randomly related objects), (b) set of singletons (pairwise
near orthogonal objects), (c) one natural cluster (uni-modal
Gaussian), (d) two natural clusters (mixture of two Gaussians)
|
|
Figure 3.2 shows CLUSION output in
four extreme scenarios to provide a feel for how data properties
translate to the visual display. Without any loss of generality, we
consider the partitioning of a set of objects into 2 clusters. For
each scenario, on the left hand side the original similarity matrix
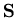 and the seriated version
and the seriated version
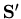 (CLUSION) for an optimal bipartitioning is shown. On the right hand
side four histograms for the distribution of similarity values
(CLUSION) for an optimal bipartitioning is shown. On the right hand
side four histograms for the distribution of similarity values 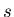 ,
which range from 0 to 1, are shown. From left to right, we have
plotted: distribution of
,
which range from 0 to 1, are shown. From left to right, we have
plotted: distribution of 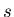 over the entire data, within the first
cluster, within the second cluster, and between first and second
cluster.
If the data is naturally clustered and the clustering algorithm is
good, then the middle two columns of plots will be much more skewed to
the right as compared to the first and fourth columns. In our
visualization this corresponds to brighter off-diagonal regions and
darker block diagonal regions in
over the entire data, within the first
cluster, within the second cluster, and between first and second
cluster.
If the data is naturally clustered and the clustering algorithm is
good, then the middle two columns of plots will be much more skewed to
the right as compared to the first and fourth columns. In our
visualization this corresponds to brighter off-diagonal regions and
darker block diagonal regions in
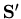 as compared to the
original
as compared to the
original
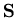 matrix.
The proposed visualization technique is quite powerful and versatile.
In figure 3.2(a) the chosen similarity behaves
randomly. Consequently, no strong visual difference between on- and
off-diagonal regions can be perceived with CLUSION in
matrix.
The proposed visualization technique is quite powerful and versatile.
In figure 3.2(a) the chosen similarity behaves
randomly. Consequently, no strong visual difference between on- and
off-diagonal regions can be perceived with CLUSION in
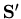 . It indicates clustering is ineffective which is
expected since there is no structure in the similarity matrix.
Figure 3.2(b) is based on data consisting of
pair-wise almost equi-distant singletons. Clustering into two groups
still renders the on-diagonal regions very bright suggesting more
splits. In fact, this will remain unchanged until each data-point
is a cluster by itself, thus, revealing the singleton character of the
data.
For monolithic data (figure 3.2(c)), many strong
similarities are indicated by an almost uniformly dark similarity
matrix
. It indicates clustering is ineffective which is
expected since there is no structure in the similarity matrix.
Figure 3.2(b) is based on data consisting of
pair-wise almost equi-distant singletons. Clustering into two groups
still renders the on-diagonal regions very bright suggesting more
splits. In fact, this will remain unchanged until each data-point
is a cluster by itself, thus, revealing the singleton character of the
data.
For monolithic data (figure 3.2(c)), many strong
similarities are indicated by an almost uniformly dark similarity
matrix
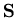 . Splitting the data results in dark off-diagonal
regions in
. Splitting the data results in dark off-diagonal
regions in
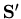 . A dark off-diagonal region suggests that
the clusters in the corresponding rows and columns should be merged
(or not be split in the first place). CLUSION indicates
that this data is actually one large cluster.
In figure 3.2(d), the gray-level distribution of
. A dark off-diagonal region suggests that
the clusters in the corresponding rows and columns should be merged
(or not be split in the first place). CLUSION indicates
that this data is actually one large cluster.
In figure 3.2(d), the gray-level distribution of
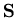 exposes bright as well as dark pixels, thereby
recommending it should be split. In this case,
exposes bright as well as dark pixels, thereby
recommending it should be split. In this case, 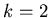 apparently is a
very good choice (and the clustering algorithm worked well) because in
apparently is a
very good choice (and the clustering algorithm worked well) because in
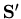 on-diagonal regions are uniformly dark and off-diagonal
regions are uniformly bright.
This induces an intuitive mining process that guides the user to the
`right' number of clusters. Too small a
on-diagonal regions are uniformly dark and off-diagonal
regions are uniformly bright.
This induces an intuitive mining process that guides the user to the
`right' number of clusters. Too small a  leaves the on-diagonal
regions inhomogeneous. On the contrary, growing
leaves the on-diagonal
regions inhomogeneous. On the contrary, growing  beyond the natural
number of clusters will introduce dark off-diagonal regions. Finally,
CLUSION can be used to visually compare the appropriateness
of different similarity measures. Let us assume, for example, that
each row in figure 3.2 illustrates a particular
way of defining similarity for the same data-set. Then, CLUSION makes visually apparent that the similarity measure in (d)
lends itself much better for clustering than the measures illustrated
in rows (a), (b), and (c).
beyond the natural
number of clusters will introduce dark off-diagonal regions. Finally,
CLUSION can be used to visually compare the appropriateness
of different similarity measures. Let us assume, for example, that
each row in figure 3.2 illustrates a particular
way of defining similarity for the same data-set. Then, CLUSION makes visually apparent that the similarity measure in (d)
lends itself much better for clustering than the measures illustrated
in rows (a), (b), and (c).




Next: Comparison
Up: CLUSION: Cluster Visualization
Previous: Coarse Seriation
Contents
Alexander Strehl
2002-05-03