



Next: Parallel Implementation
Up: System Issues
Previous: Synergy between OPOSSUM and
Contents
FASTOPOSSUM
Since OPOSSUM aims to achieve balanced clusters, random
sampling is effective for obtaining adequate examples of each cluster.
If the clusters are perfectly balanced, the distribution of the number
of samples from a specific cluster in a subsample of size
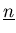 taken from the entire population is binomial with mean
taken from the entire population is binomial with mean
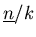 and variance
and variance
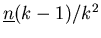 . For finite
population, the variance will be even less. Thus, if we require at
least
. For finite
population, the variance will be even less. Thus, if we require at
least 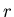 representatives from this cluster, then the number of
samples is given by:
representatives from this cluster, then the number of
samples is given by:
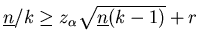 , where
, where
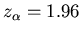 or 2.81
for 97.5% and 99.5% confidence levels respectively. This is
or 2.81
for 97.5% and 99.5% confidence levels respectively. This is
 . For example, if we have 10 clusters and need to ensure at
least 20 representatives from a given cluster with probability 0.995,
about 400 samples are adequate. Note that this number is independent
of
. For example, if we have 10 clusters and need to ensure at
least 20 representatives from a given cluster with probability 0.995,
about 400 samples are adequate. Note that this number is independent
of  if
if 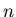 is adequately large (at least 400 in this case), so even
for over one million customers, only 400 representatives are required.
This suggests a simple and effective way to scale OPOSSUM
to very large number of objects
is adequately large (at least 400 in this case), so even
for over one million customers, only 400 representatives are required.
This suggests a simple and effective way to scale OPOSSUM
to very large number of objects 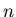 , using the following four-step
process called FASTOPOSSUM:
, using the following four-step
process called FASTOPOSSUM:
- Pick a boot-sample of size
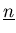 so that the
corresponding
so that the
corresponding 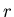 value is adequate to define each cluster.
value is adequate to define each cluster.
- Apply OPOSSUM to the boot-sample to get
 initial
clusters.
initial
clusters.
- Find the centroid for each of the
 clusters.
clusters.
- Assign each of the remaining
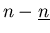 points
to the cluster with the nearest centroid.
points
to the cluster with the nearest centroid.
Using
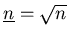 reduces the complexity of FASTOPOSSUM
to
reduces the complexity of FASTOPOSSUM
to 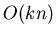 . Note that the above algorithm may not result
in balanced clusters. We can enforce balancing by allocating the
remaining points to the
. Note that the above algorithm may not result
in balanced clusters. We can enforce balancing by allocating the
remaining points to the  clusters in groups, each time solving a
stable marriage problem [GI89], but this will increase the
computation time.
Figure 3.8 illustrates the behavior of FASTOPOSSUM
for the drugstore customer data-set from subsection
3.5.1. The remaining edge weight fraction indicates how much of the
cumulative edge weight remains after the edge separator has been
removed:
clusters in groups, each time solving a
stable marriage problem [GI89], but this will increase the
computation time.
Figure 3.8 illustrates the behavior of FASTOPOSSUM
for the drugstore customer data-set from subsection
3.5.1. The remaining edge weight fraction indicates how much of the
cumulative edge weight remains after the edge separator has been
removed:
 The better the partitioning, the smaller the edge-separator, and thus
the larger the remaining edge weight fraction. Surprisingly the
speedup does not result in a significant decreased quality in terms of
remaining edge weight (figure 3.8(a)). However, the
balancing property is progressively relaxed as the boot-sample becomes
smaller in comparison to the full data-set (figure
3.8(b)). Using
The better the partitioning, the smaller the edge-separator, and thus
the larger the remaining edge weight fraction. Surprisingly the
speedup does not result in a significant decreased quality in terms of
remaining edge weight (figure 3.8(a)). However, the
balancing property is progressively relaxed as the boot-sample becomes
smaller in comparison to the full data-set (figure
3.8(b)). Using
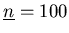 initial points
reduces the original computation time to less than 1% at comparable
remaining edge weight but at an imbalance of 3.5 in the worst of 10
random trials.
initial points
reduces the original computation time to less than 1% at comparable
remaining edge weight but at an imbalance of 3.5 in the worst of 10
random trials.
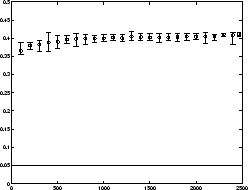
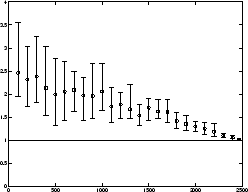
Figure 3.8:
Effect of sub-sampling on OPOSSUM.
Cluster quality as measured by remaining edge weight fraction (a) and
imbalance (b) of total graph with 2466 vertices (customers from
subsection 3.5.1) for various boot-sample sizes in
FASTOPOSSUM. For each setting the results' range and mean
of 10 trials are depicted.
Using all 2466 customers as the boot-sample (i.e., no sub-sampling)
results in balancing within the 1.05 imbalance requirement and
approximately 40% of edge weight remaining (as compared to 5%
baseline for random clustering). As the boot-sample becomes smaller
the remaining edge weight stays approximately the same (a), however
the imbalance increases (b).
 |
 |
| (a) |
(b) |
|
These results indicate that scaling to large 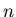 is easily possible,
if one is willing to relax the balancedness constraints.
is easily possible,
if one is willing to relax the balancedness constraints.




Next: Parallel Implementation
Up: System Issues
Previous: Synergy between OPOSSUM and
Contents
Alexander Strehl
2002-05-03
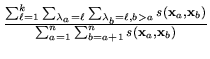 The better the partitioning, the smaller the edge-separator, and thus
the larger the remaining edge weight fraction. Surprisingly the
speedup does not result in a significant decreased quality in terms of
remaining edge weight (figure 3.8(a)). However, the
balancing property is progressively relaxed as the boot-sample becomes
smaller in comparison to the full data-set (figure
3.8(b)). Using
The better the partitioning, the smaller the edge-separator, and thus
the larger the remaining edge weight fraction. Surprisingly the
speedup does not result in a significant decreased quality in terms of
remaining edge weight (figure 3.8(a)). However, the
balancing property is progressively relaxed as the boot-sample becomes
smaller in comparison to the full data-set (figure
3.8(b)). Using