Next: Current Challenges in Clustering
Up: Introduction
Previous: Notation
Contents
Relationship-based Clustering Approach
The pattern recognition process from raw data to knowledge is
characterized by a large reduction of description length by
multiple orders of magnitude. A step-wise approach that includes several
distinct levels of abstraction is generally adopted. A common
framework can be observed for most systems as the input is transformed
through the following spaces1.2:
- Input space
 .
.
- Clustering is based on observations
about the objects under consideration. The input space captures all
the known raw information about the object, such as a
customer's purchase history, a hypertext document, a grid of
gray-level values for a visual image, or a sequence of DNA. Let
 denote the number of objects in the input space, and let a particular
object have
denote the number of objects in the input space, and let a particular
object have  associated attributes. The number of attributes can
vary by object. For example, objects can be characterized by
variable length sequences.
associated attributes. The number of attributes can
vary by object. For example, objects can be characterized by
variable length sequences.
- Feature space
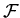 .
.
- The transformation
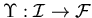 removes some redundancy by
feature selection or extraction. In feature selection, a
subset of the input dimensions that is highly relevant to the learning
problem is selected. In document clustering, for example, a variety of
word selection and weighting schemes have been proposed
[YP97,Kol97]. A feature extraction transformation may
extract the locations of edge elements from a gray-level image. Other
popular transformations include the Fourier transformation for speech
processing and the Singular Value Decomposition (SVD) for multivariate
statistical data. Features (or attributes) may be distinguished by
the type and number of values they can take: We distinguish binary
(Boolean true / false decision, such as married), nominal (finite
number of categorical labels with no inherent order, such as color), ordinal (mappable to the cardinal numbers with a smallest
element and an ordering relation, such as rank), continuous
(real valued measurements such as latitude), and combinations
thereof. The transformation to feature space may render some objects
unusable, due to missing data or non-compliance with input
constraints. Thus, we denote the corresponding number of objects as
removes some redundancy by
feature selection or extraction. In feature selection, a
subset of the input dimensions that is highly relevant to the learning
problem is selected. In document clustering, for example, a variety of
word selection and weighting schemes have been proposed
[YP97,Kol97]. A feature extraction transformation may
extract the locations of edge elements from a gray-level image. Other
popular transformations include the Fourier transformation for speech
processing and the Singular Value Decomposition (SVD) for multivariate
statistical data. Features (or attributes) may be distinguished by
the type and number of values they can take: We distinguish binary
(Boolean true / false decision, such as married), nominal (finite
number of categorical labels with no inherent order, such as color), ordinal (mappable to the cardinal numbers with a smallest
element and an ordering relation, such as rank), continuous
(real valued measurements such as latitude), and combinations
thereof. The transformation to feature space may render some objects
unusable, due to missing data or non-compliance with input
constraints. Thus, we denote the corresponding number of objects as
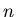 (
(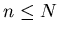 ) and the number of dimensions by
) and the number of dimensions by 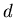 (
(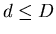 ).
).
- Similarity space
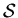
- is an optional intermediate
space between the feature space
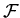 and the output space
and the output space
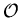 . The similarity transformation
. The similarity transformation
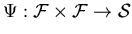 translates a pair of
internal, object-centered descriptions in terms of features into
an external, relationship-oriented space
translates a pair of
internal, object-centered descriptions in terms of features into
an external, relationship-oriented space
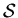 . While
there are
. While
there are 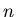
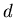 -dimensional descriptions (e.g.,
-dimensional descriptions (e.g.,
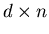 matrix
matrix
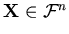 ) there are
) there are
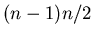 pairwise
relations (e.g., symmetric
pairwise
relations (e.g., symmetric
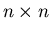 matrix
matrix
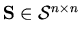 ).
In our work, we mainly use similarities
).
In our work, we mainly use similarities
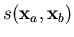 because they induce mathematically convenient and efficient sparse
matrix constructs. Instead of minimizing the cost, we maximize
accumulated similarity. The dual notions of distance and similarity
can be interchanged. However, their conversion has to be done
carefully in order to preserve critical properties as will be
discussed later. Similarities
because they induce mathematically convenient and efficient sparse
matrix constructs. Instead of minimizing the cost, we maximize
accumulated similarity. The dual notions of distance and similarity
can be interchanged. However, their conversion has to be done
carefully in order to preserve critical properties as will be
discussed later. Similarities
![$ s\in [0,1] \subset
\mathbb{R}$](img41.png) and distances
and distances
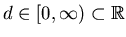 can be
related in various non-linear, monotonically decreasing ways.
can be
related in various non-linear, monotonically decreasing ways.
- Output space
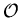 .
.
- In partitioning, the output
space is a vector of nominal attributes providing cluster membership
to one of
 clusters. To represent
a clustering, we denote it either as a set of clusters
clusters. To represent
a clustering, we denote it either as a set of clusters
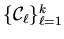 or as a
or as a 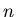 -dimensional label
vector
-dimensional label
vector
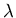 , where
, where
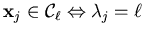 . Many approaches to the output
transformation
. Many approaches to the output
transformation
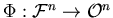 (or
(or
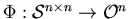 ), the actual clustering algorithm, have been
investigated. The next chapter will give an overview.
), the actual clustering algorithm, have been
investigated. The next chapter will give an overview.
- Hypothesis space
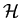
- is the space where a particular
clustering algorithm searches for a solution.
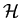 depends
on the language bias of the clustering algorithm. A given
algorithm can be viewed as looking for an optimal solution (at maximum
objective or minimum cost as given by the evaluation function)
according to its search bias.
An evaluation function
depends
on the language bias of the clustering algorithm. A given
algorithm can be viewed as looking for an optimal solution (at maximum
objective or minimum cost as given by the evaluation function)
according to its search bias.
An evaluation function
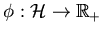 can work purely based on the feature and/or similarity space, but can also
incorporate external knowledge (such as user given categorizations).
can work purely based on the feature and/or similarity space, but can also
incorporate external knowledge (such as user given categorizations).
Let us look at the output space in a little more detail.
In this work, we focus on flat clusterings (partitions) for a variety
of reasons. Any hierarchical clustering can be conducted as a
series of flat clusterings, rendering flat clustering the more
fundamental step.
Hierarchical complete  -ary trees of depth
-ary trees of depth  can be encoded
without loss of information as a single ordered flat labeling with
can be encoded
without loss of information as a single ordered flat labeling with
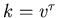 clusters. To obtain the clustering on layer
clusters. To obtain the clustering on layer
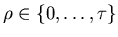 , each of the
, each of the 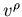 disjoint intervals
of labels (with length
disjoint intervals
of labels (with length
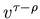 starting at label 1)
have to be collapsed to a single label (considered one cluster).
(consider e.g.,
starting at label 1)
have to be collapsed to a single label (considered one cluster).
(consider e.g., 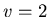 ,
, 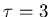 , so the labels are structured in a
tree as follows:
, so the labels are structured in a
tree as follows:
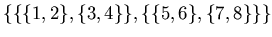 ) Consequently, a flat
labeling with implicit ordering information is just as expressive as
full hierarchical cluster trees. But let us return to labelings without
ordering information.
) Consequently, a flat
labeling with implicit ordering information is just as expressive as
full hierarchical cluster trees. But let us return to labelings without
ordering information.
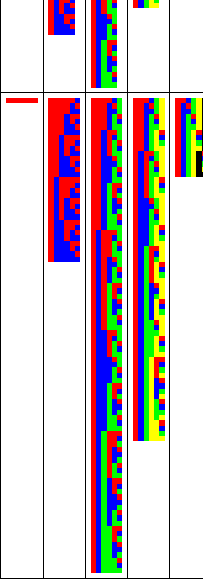
Figure 1.1:
All possible clusterings
of up to 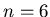 objects (rows top to bottom) into up to
objects (rows top to bottom) into up to 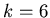 groups
(columns left to right). In each table cell a matrix shows all
clusterings for a particular choice of
groups
(columns left to right). In each table cell a matrix shows all
clusterings for a particular choice of 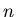 and
and  . A matrix shows
one clustering per row. The color in the
. A matrix shows
one clustering per row. The color in the 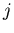 -th column indicates the
group membership of the
-th column indicates the
group membership of the 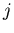 -th object. Group association is shown in
red, blue, green, black, and gray.
-th object. Group association is shown in
red, blue, green, black, and gray.
|
|
Figure 1.1 illustrates all clusterings for less
than 6 objects and clusters. For example, there are 90 partitionings
of 6 objects into 3 groups. In general, for a flat clustering of 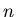 objects into
objects into  partitions there are
partitions there are
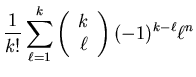 |
(1.1) |
possible partitionings, or approximately 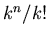 for
for 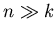 .
Clearly, the exponentially growing search space makes an exhaustive,
global search prohibitive. In general, clustering problems have
difficult, non-convex, objective functions modeling the similarity
within clusters and the dissimilarity between clusters. In general,
the clustering problem is NP-hard [HJ97].
.
Clearly, the exponentially growing search space makes an exhaustive,
global search prohibitive. In general, clustering problems have
difficult, non-convex, objective functions modeling the similarity
within clusters and the dissimilarity between clusters. In general,
the clustering problem is NP-hard [HJ97].
Figure 1.2:
Object-centered (top) versus relationship-based clustering (bottom).
The focus in this dissertation is on relationship-based clustering
which is independent of the feature space.
|
|
In this dissertation, the focus is on the similarity space. Most
standard algorithms spend little attention on the similarity
space. Rather, similarity computations are directly integrated into the
clustering algorithms which proceeds straight from feature space to
the output space. The introduction of an independent modular
similarity space has many advantages, as it allows us to address many
of the challenges discussed in the next section. We call this
approach similarity-based or relationship-based or graph-based.
Figure 1.2 contrasts the object-centered with the
relationship-based approach. The key difference between
relationship-based clustering and regular clustering is the focus on
the similarity space
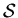 instead of working directly in the
feature domain
instead of working directly in the
feature domain
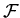 .
.
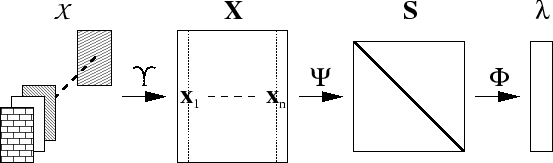
Figure 1.3:
Abstract overview of the
general relationship-based,
single-layer, single-learner, batch clustering process from a set of
raw object descriptions
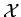 to the vector of cluster labels
to the vector of cluster labels
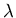 :
:
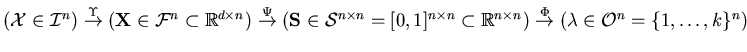
|
|
In figure 1.3 an abstract overview of the
general relationship-based framework is shown. In web-page
clustering, for example,
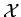 is a collection of
is a collection of 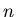 web-pages. Extracting features yields
web-pages. Extracting features yields
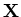 , for example, the
term frequencies of stemmed words, normalized such that
, for example, the
term frequencies of stemmed words, normalized such that
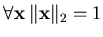 . Similarities are computed,
using e.g., cosine based similarity
. Similarities are computed,
using e.g., cosine based similarity 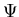 yielding the
yielding the
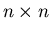 similarity matrix
similarity matrix
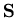 . Finally,
. Finally, 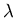 is computed using
e.g., graph partitioning.
is computed using
e.g., graph partitioning.




Next: Current Challenges in Clustering
Up: Introduction
Previous: Notation
Contents
Alexander Strehl
2002-05-03
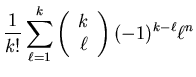
![]() instead of working directly in the
feature domain
instead of working directly in the
feature domain
![]() .
.