Cluster-based Similarity Partitioning Algorithm (CSPA)

Essentially, if two objects are in the same cluster then they are considered to be fully similar, and if not they are dissimilar. This is the simplest heuristic and is used in the Cluster-based Similarity Partitioning Algorithm (CSPA). With this viewpoint, one can simply reverse engineer a single clustering into a binary similarity matrix. Similarity between two objects is 1 if they are in the same cluster and 0 otherwise. 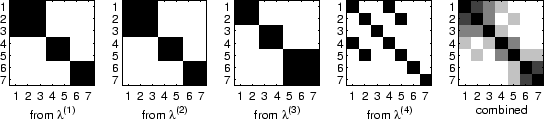For each clustering, a $n \times n$ binary similarity matrix is created. The entry-wise average of $r$ such matrices representing the $r$ sets of groupings yields an overall similarity matrix. Figure 5.3 illustrates the generation of the cluster-based similarity matrix for the example given in table 5.1.

Alternatively, and more concisely, this can be interpreted as using $k$ binary cluster membership features and defining similarity as the fraction of clusterings in which two objects are in the same cluster. The entire $n \times n$ similarity matrix $\mathbf{S}$ can be computed in one sparse matrix multiplication $\mathbf{S} = \frac{1}{r} \mathbf{H} \mathbf{H}^{\dagger}$.^5.4

Now, we can use the similarity matrix to recluster the objects using any reasonable similarity based clustering algorithm. We chose to partition the induced similarity graph (vertex = object, edge weight = similarity) using METIS [KK98a] because of its robust and scalable properties.

Figure 5.3: Illustration of Cluster-based Similarity Partitioning Algorithm (CSPA) for the cluster ensemble example problem given in table 5.1. Each clustering contributes a similarity matrix (matrix entries are shown by darkness proportional to similarity). Their average is then used to recluster the objects to yield consensus.