The second algorithm is a direct approach to cluster ensembles that
re-partitions the data using the given clusters as indications of
strong bonds.
The cluster ensemble problem is formulated as partitioning the
hypergraph by cutting a minimal number of hyperedges. We call
this approach the HyperGraph Partitioning Algorithm (HGPA). All
hyperedges are considered to have the same weight. Also, all vertices
are equally weighted. Note, that this includes ![]() -way
relationship information, while CSPA only considers pairwise
relationships.
Now, we look for a hyperedge separator that partitions the hypergraph
(figure 5.4) into
-way
relationship information, while CSPA only considers pairwise
relationships.
Now, we look for a hyperedge separator that partitions the hypergraph
(figure 5.4) into ![]() unconnected components
of approximately the same size. Equal sizes are obtained by
maintaining a vertex imbalance of at most 5% as formulated by the
following constraint:
unconnected components
of approximately the same size. Equal sizes are obtained by
maintaining a vertex imbalance of at most 5% as formulated by the
following constraint:
![]() .
.
Hypergraph partitioning is a well-studied area
[KL70,AK95] and algorithmic details are omitted
here for brevity.
We use the hypergraph partitioning package HMETIS
[KAKS97]. HMETIS gives high-quality partitions and is very
scalable.
However, please note that hypergraph partitioning in general has no
provision for partially cut hyperedges. This means that there is no
sensitivity to how much of a hyperedge is left in the same group
after the cut. This can be problematic for our applications.
Let us consider the example from table
5.1. For simplicity, let us assume that
only the three hyperedges from
![]() are present.
The two partitionings
are present.
The two partitionings
![]() and
and
![]() both cut
all three hyperedges. The first is intuitively superior, because 2/3
of the hyperedge
both cut
all three hyperedges. The first is intuitively superior, because 2/3
of the hyperedge
![]() `remain' versus only 1/3 in the
second. However, in standard hypergraph partitioning they have
equivalent quality since both cut the same number of hyperedges.
`remain' versus only 1/3 in the
second. However, in standard hypergraph partitioning they have
equivalent quality since both cut the same number of hyperedges.
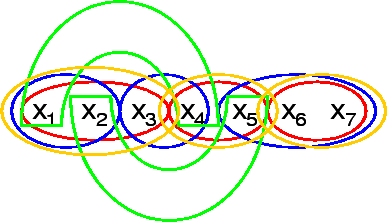
|