Next: Discussion and Comparison
Up: Efficient Consensus Functions
Previous: HyperGraph Partitioning Algorithm (HGPA)
Contents
Meta-CLustering Algorithm (MCLA)
In this subsection, we introduce the third algorithm to solve the
cluster ensemble problem. The Meta-CLustering Algorithm (MCLA) is
based on clustering clusters. It also yields object-wise confidence
estimates of cluster membership.
We represented each cluster by a hyperedge. The idea in MCLA is to
group and collapse related hyperedges and assign each object to the
collapsed hyperedge in which it participates most strongly. The
hyperedges that are considered related for the purpose of collapsing
are determined by a graph-based clustering of hyperedges. We refer to
each cluster of hyperedges as a meta-cluster
 . Collapsing reduces the number of
hyperedges from
. Collapsing reduces the number of
hyperedges from
 to
to  .
The detailed steps are:
.
The detailed steps are:
- Construct Meta-graph.
- Let us view all the
 indicator vectors
indicator vectors
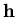 (the hyperedges of
(the hyperedges of
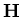 ) as
vertices of another regular undirected graph, the meta-graph. The edge
weights are proportional to the similarity between vertices. A
suitable similarity measure here is the binary Jaccard measure, since
it is the ratio of the intersection to the union of the sets of
objects corresponding to the two hyperedges. Formally, the edge
weight
) as
vertices of another regular undirected graph, the meta-graph. The edge
weights are proportional to the similarity between vertices. A
suitable similarity measure here is the binary Jaccard measure, since
it is the ratio of the intersection to the union of the sets of
objects corresponding to the two hyperedges. Formally, the edge
weight 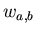 between two vertices
between two vertices 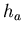 and
and 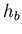 as defined by
the binary Jaccard measure of the corresponding indicator vectors
as defined by
the binary Jaccard measure of the corresponding indicator vectors
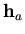 and
and
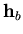 is:
is:
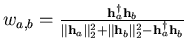 .
.
Since the clusters are non-overlapping (e.g., hard), there are no edges
amongst vertices of the same clustering
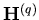 and, thus,
the meta-graph is
and, thus,
the meta-graph is 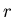 -partite, as shown in figure
5.5.
-partite, as shown in figure
5.5.
- Cluster Hyperedges.
- Find matching labels by partitioning the meta-graph into
 balanced
meta-clusters.
Each vertex is weighted proportional
to the size of the corresponding cluster.
Balancing ensures that the sum of vertex-weights is approximately
the same in each meta-cluster.
We use the graph partitioning package METIS in this step.
This results in a clustering of the
balanced
meta-clusters.
Each vertex is weighted proportional
to the size of the corresponding cluster.
Balancing ensures that the sum of vertex-weights is approximately
the same in each meta-cluster.
We use the graph partitioning package METIS in this step.
This results in a clustering of the
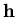 vectors.
Since each vertex in the meta-graph represents a distinct cluster label, a
meta-cluster represents a group of corresponding labels.
vectors.
Since each vertex in the meta-graph represents a distinct cluster label, a
meta-cluster represents a group of corresponding labels.
- Collapse Meta-clusters.
- For each of the
 meta-clusters, we collapse the hyperedges into a
single meta-hyperedge. Each meta-hyperedge has an association vector
which contains an entry for each object describing its level of
association with the corresponding meta-cluster. The level is
computed by averaging all indicator vectors
meta-clusters, we collapse the hyperedges into a
single meta-hyperedge. Each meta-hyperedge has an association vector
which contains an entry for each object describing its level of
association with the corresponding meta-cluster. The level is
computed by averaging all indicator vectors
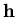 of a
particular meta-cluster.5.5
An entry of 0 or 1 indicates the weakest or
strongest association, respectively.
of a
particular meta-cluster.5.5
An entry of 0 or 1 indicates the weakest or
strongest association, respectively.
- Compete for Objects.
- In this step, each object is assigned to its
most associated meta-cluster:
Specifically, an object is assigned to the meta-cluster with the highest
entry in the association vector. Ties are broken
randomly. The confidence of an assignment is reflected by the
winner's share of association (ratio of the winner's association to
the sum of all other associations). Note that not every
meta-cluster can be guaranteed to win at least one object. Thus,
there are at most
 labels in the final combined clustering
labels in the final combined clustering
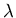 .
.
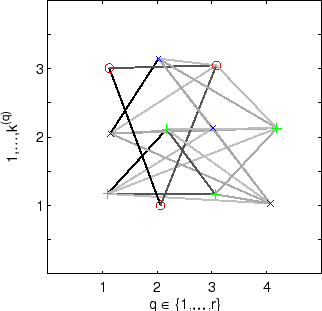
Figure 5.5 illustrates meta-clustering
for the example given in table
5.1 where 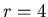 ,
, 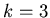 ,
,
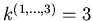 , and
, and 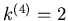 . Figure
5.5 shows the original 4-partite meta-graph.
The three meta-clusters are shown in red /
. Figure
5.5 shows the original 4-partite meta-graph.
The three meta-clusters are shown in red /  , blue /
, blue /  , and
green /
, and
green /  .
Consider the first meta-cluster,
.
Consider the first meta-cluster,
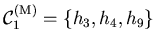 (the red/
(the red/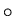 markers in figure
5.5). Collapsing the hyperedges yields the
object-weighted meta-hyperedge
markers in figure
5.5). Collapsing the hyperedges yields the
object-weighted meta-hyperedge
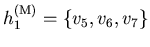 with association vector
with association vector
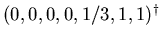 . Subsequently, meta-cluster
. Subsequently, meta-cluster
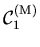 will win the competition for
vertices/objects
will win the competition for
vertices/objects 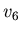 and
and 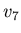 , and thus represent the cluster
, and thus represent the cluster
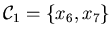 in the resulting integrated clustering.
Our proposed meta-clustering algorithm robustly outputs
in the resulting integrated clustering.
Our proposed meta-clustering algorithm robustly outputs
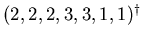 , one of the 6 optimal clusterings which is
equivalent to clusterings
, one of the 6 optimal clusterings which is
equivalent to clusterings
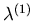 and
and
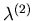 . The uncertainty about some objects is
reflected in the confidences 3/4, 1, 2/3, 1, 1/2, 1, and 1 for objects
1 through 7, respectively.
. The uncertainty about some objects is
reflected in the confidences 3/4, 1, 2/3, 1, 1/2, 1, and 1 for objects
1 through 7, respectively.
Figure 5.5:
Illustration of Meta-CLustering Algorithm (MCLA) for
the cluster ensemble example problem given in table
5.1.
The 4-partite meta-graph is shown. Edge darkness increases with edge
weight. The vertex positions are slightly perturbed to
expose otherwise occluded edges. The three meta-clusters are shown in
red /  , blue /
, blue / 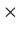 , and green /
, and green / 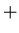 .
.
|
|




Next: Discussion and Comparison
Up: Efficient Consensus Functions
Previous: HyperGraph Partitioning Algorithm (HGPA)
Contents
Alexander Strehl
2002-05-03
![]() . Collapsing reduces the number of
hyperedges from
. Collapsing reduces the number of
hyperedges from
![]() to
to ![]() .
The detailed steps are:
.
The detailed steps are:
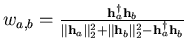 .
.
![]() and, thus,
the meta-graph is
and, thus,
the meta-graph is ![]() -partite, as shown in figure
5.5.
-partite, as shown in figure
5.5.
![]() ,
, ![]() ,
,
![]() , and
, and ![]() . Figure
5.5 shows the original 4-partite meta-graph.
The three meta-clusters are shown in red /
. Figure
5.5 shows the original 4-partite meta-graph.
The three meta-clusters are shown in red / ![]() , blue /
, blue / ![]() , and
green /
, and
green / ![]() .
Consider the first meta-cluster,
.
Consider the first meta-cluster,
![]() (the red/
(the red/![]() markers in figure
5.5). Collapsing the hyperedges yields the
object-weighted meta-hyperedge
markers in figure
5.5). Collapsing the hyperedges yields the
object-weighted meta-hyperedge
![]() with association vector
with association vector
![]() . Subsequently, meta-cluster
. Subsequently, meta-cluster
![]() will win the competition for
vertices/objects
will win the competition for
vertices/objects ![]() and
and ![]() , and thus represent the cluster
, and thus represent the cluster
![]() in the resulting integrated clustering.
Our proposed meta-clustering algorithm robustly outputs
in the resulting integrated clustering.
Our proposed meta-clustering algorithm robustly outputs
![]() , one of the 6 optimal clusterings which is
equivalent to clusterings
, one of the 6 optimal clusterings which is
equivalent to clusterings
![]() and
and
![]() . The uncertainty about some objects is
reflected in the confidences 3/4, 1, 2/3, 1, 1/2, 1, and 1 for objects
1 through 7, respectively.
. The uncertainty about some objects is
reflected in the confidences 3/4, 1, 2/3, 1, 1/2, 1, and 1 for objects
1 through 7, respectively.